题目内容
F1，F2是椭圆C：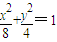
的焦点，在C上满足PF1⊥PF2的点P的个数为 ．
【答案】分析：法一（代数法）：设|PF1|=m，|PF2|=n，根据椭圆的性质可知m+n=2a，又根据PF1⊥PF2可知m2+n2=（2c）2，进而求得mn，所以m，n是一元二次方程x2-4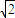
x+8=0的两根，根据判别式可知方程有一个根，再根据椭圆的对称性可知应有2个点满足．
法二（几何法）：由图形知，∠F1BF2=90，故这样的P点只能有两个．
解答：解：设|PF1|=m，|PF2|=n
则m+n=2a=4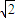
，m2+n2=（2c）2=16
∴mn=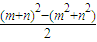
=8
所以m，n是一元二次方程x2-4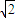
x+8=0的两根
判别式△=32-32=0故此方程有一个实根，
根据椭圆的对称性可知椭圆上存在2个点P满足PF1⊥PF2
故答案为2．
法二：（几何法）由椭圆的图形知∠F1BF2=90，故这样的P点只能有两个．
故答案为2．
点评：本题主要考查了椭圆的基本性质，属基础题．
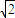x+8=0的两根，根据判别式可知方程有一个根，再根据椭圆的对称性可知应有2个点满足．法二（几何法）：由图形知，∠F1BF2=90，故这样的P点只能有两个．
解答：解：设|PF1|=m，|PF2|=n
则m+n=2a=4
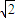，m2+n2=（2c）2=16∴mn=
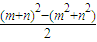=8所以m，n是一元二次方程x2-4
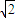x+8=0的两根判别式△=32-32=0故此方程有一个实根，
根据椭圆的对称性可知椭圆上存在2个点P满足PF1⊥PF2
故答案为2．
法二：（几何法）由椭圆的图形知∠F1BF2=90，故这样的P点只能有两个．
故答案为2．
点评：本题主要考查了椭圆的基本性质，属基础题．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
（2012•鹰潭一模）如图，已知F1，F2是椭圆