题目内容
7.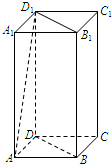 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB.(1)求AD1与面BB1D1D所成角的正弦值;
(2)点E在侧棱AA1上,若二面角E-BD-C1的余弦值为$\frac{{\sqrt{3}}}{3}$,求$\frac{AE}{{A{A_1}}}$的值.
分析 (1)建立空间直角坐标系,求出平面的法向量,利用向量法即可求AD1与面BB1D1D所成角的正弦值;
(2)求出平面的法向量,根据二面角与平面法向量之间的关系进行求解即可.
解答  解:(1)以D为原点,DA,DC,DD1分别为x轴,y轴,z轴,建立如图所示空间直角坐标系D-xyz.
解:(1)以D为原点,DA,DC,DD1分别为x轴,y轴,z轴,建立如图所示空间直角坐标系D-xyz.
设AB=1,则D(0,0,0),A(1,0,0),
B(1,1,0),C(0,1,0),D1(0,0,2),
A1(1,0,2),B1(1,1,2),C1(0,1,2).
(1)设AD1与面BB1D1D所成角的大小为θ,$\overrightarrow{A{D_1}}=(-1,0,2)$,
设平面BB1D1D的法向量为$\overrightarrow{n}$=(x,y,z),$\overrightarrow{DB}=(1,1,0)$,$\overrightarrow{D{D_1}}=(0,0,2)$,
则$\overrightarrow{n}$$•\overrightarrow{DB}$=0,$\overrightarrow{n}•\overrightarrow{D{D}_{1}}=0$,即x+y=0,z=0.
令x=1,则y=-1,所以n=(1,-1,0),
sinθ=|cos<$\overrightarrow{A{D}_{1}},\overrightarrow{n}$>|=$\frac{|\overrightarrow{A{D}_{1}}•\overrightarrow{n}|}{|\overrightarrow{A{D}_{1}}||\overrightarrow{n}|}$=$\frac{\sqrt{10}}{10}$,
所以AD1与平面BB1D1D所成角的正弦值为$\frac{{\sqrt{10}}}{10}$.
(2)设E(1,0,λ),0≤λ≤2.
设平面EBD的法向量为$\overrightarrow{{n}_{1}}$=(x1,y1,z1),平面BDC1的法向量为$\overrightarrow{{n}_{2}}$=(x2,y2,z2),$\overrightarrow{DB}=(1,1,0),\overrightarrow{DE}=(1,0,λ)$,
由$\overrightarrow{{n}_{1}}•\overrightarrow{DB}=0$,$\overrightarrow{{n}_{1}}•\overrightarrow{DE}$=0,得x1+y1=0,x1+λz1=0,
令z1=1,则x1=-λ,y1=λ,n1=(-λ,λ,1),$\overrightarrow{D{C_1}}=(0,1,2)$,
由$\overrightarrow{{n}_{2}}•\overrightarrow{DB}=0$,$\overrightarrow{{n}_{2}}•\overrightarrow{D{C}_{1}}=0$,得x2+y2=0,y2+2z2=0,
令z2=1,则x2=2,y2=-2,n2=(2,-2,1),
cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{1-4λ}{3\sqrt{2{λ}^{2}+1}}$,
所以$\frac{{\sqrt{3}}}{3}=|\frac{1-4λ}{{3\sqrt{2{λ^2}+1}}}|$,得λ=1.
所以$\frac{AE}{{A{A_1}}}=\frac{1}{2}$.
点评 本题主要考查直线和平面所成角的求解以及二面角的应用,建立坐标系,利用向量法是解决空间角的常用方法.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
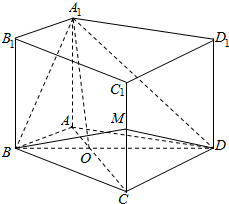 如图所示,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,BD⊥AC于O,且AA1=OC=2OA=4,点M是棱CC1上一点.
如图所示,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,BD⊥AC于O,且AA1=OC=2OA=4,点M是棱CC1上一点.