题目内容
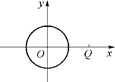
如图,已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于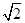 .求动点M的轨迹方程,并说明它表示什么.
.求动点M的轨迹方程,并说明它表示什么.
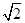 .求动点M的轨迹方程,并说明它表示什么.
.求动点M的轨迹方程,并说明它表示什么.
(x-4)2+y2=7.它表示圆,
设直线MN切圆于N,则动点M组成的集合是P={M||MN|=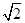 |MQ|}.
|MQ|}.
因为圆的半径|ON|=1,所以|MN|2=|MO|2-1.
设点M的坐标为(x,y),则 ,整理得(x-4)2+y2=7.
,整理得(x-4)2+y2=7.
它表示圆,该圆圆心的坐标为(4,0),半径为 .
.
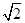 |MQ|}.
|MQ|}.因为圆的半径|ON|=1,所以|MN|2=|MO|2-1.
设点M的坐标为(x,y),则
 ,整理得(x-4)2+y2=7.
,整理得(x-4)2+y2=7.它表示圆,该圆圆心的坐标为(4,0),半径为
 .
.
练习册系列答案
相关题目
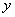 轴所得弦长为
轴所得弦长为 ;②被
;②被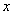 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为 ;③圆心到直线
;③圆心到直线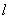 :
: 的距离为
的距离为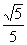 的圆的方程。
的圆的方程。 (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.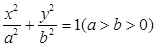 的左、右焦点分别为
的左、右焦点分别为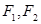 ,点
,点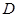 在椭圆上,
在椭圆上,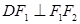 ,
, ,
,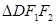 的面积为
的面积为 .
.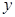 轴上的圆,使圆在
轴上的圆,使圆在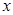 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
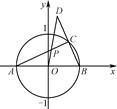
 :
: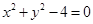 ,圆
,圆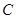 :
: ,若圆
,若圆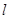 交圆
交圆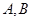 两点,则
两点,则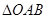 面积的取值范围是
面积的取值范围是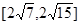
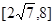
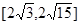

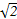 <m<2
<m<2