题目内容
已知函数 ,
,
(1)求函数 的定义域;
的定义域;
(2)求函数 在区间
在区间 上的最小值;
上的最小值;
(3)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式 对函数
对函数 的定义域上的任意
的定义域上的任意 恒成立;命题q:指数函数
恒成立;命题q:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
 ,
,(1)求函数
 的定义域;
的定义域;(2)求函数
 在区间
在区间 上的最小值;
上的最小值;(3)已知
 ,命题p:关于x的不等式
,命题p:关于x的不等式 对函数
对函数 的定义域上的任意
的定义域上的任意 恒成立;命题q:指数函数
恒成立;命题q:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.(1)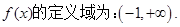 (2)
(2)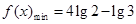
(3)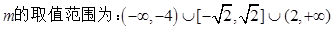
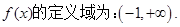 (2)
(2)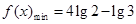
(3)
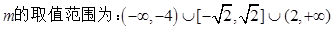
第一问中,利用由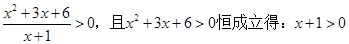 即
即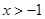

第二问中,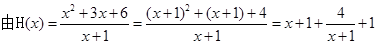 ,
,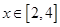 得:
得:
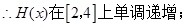
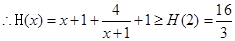 ,
,
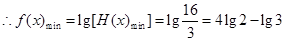
第三问中,由在函数 的定义域上 的任意
的定义域上 的任意 ,
,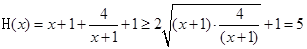 ,当且仅当
,当且仅当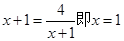 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,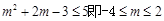 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时;当命题p为假,命题q为真时分为两种情况讨论即可 。
解:(1)由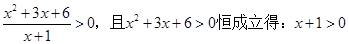 即
即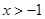

(2)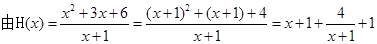 ,
,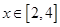 得:
得:
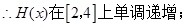
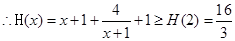 ,
,

(3)由在函数 的定义域上 的任意
的定义域上 的任意 ,
,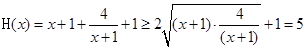 ,当且仅当
,当且仅当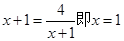 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,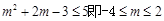 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时,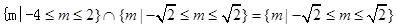
当命题p为假,命题q为真时,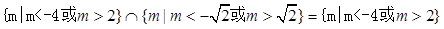 ,
,
所以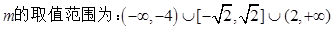
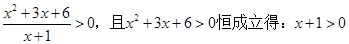 即
即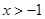

第二问中,
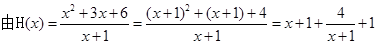 ,
,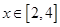 得:
得: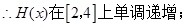
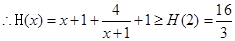 ,
,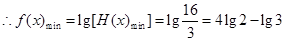
第三问中,由在函数
 的定义域上 的任意
的定义域上 的任意 ,
,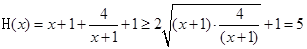 ,当且仅当
,当且仅当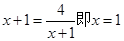 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,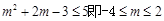 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以当命题p为真,命题q为假时;当命题p为假,命题q为真时分为两种情况讨论即可 。
解:(1)由
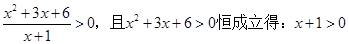 即
即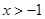

(2)
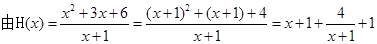 ,
,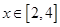 得:
得: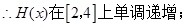
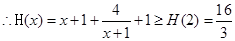 ,
,
(3)由在函数
 的定义域上 的任意
的定义域上 的任意 ,
,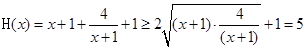 ,当且仅当
,当且仅当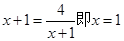 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,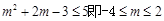 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以当命题p为真,命题q为假时,
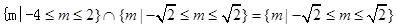
当命题p为假,命题q为真时,
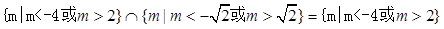 ,
,所以
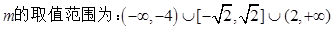

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ”;
”; ,则
,则
 为假命题,则
为假命题,则 ,
, 均为假命题;
均为假命题; 的充分不必要条件.
的充分不必要条件.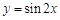 的最小正周期为
的最小正周期为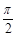 ;命题q:函数
;命题q:函数 的图象关于直线
的图象关于直线 对称.则下列判断正确的是
对称.则下列判断正确的是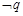 为假
为假 为假
为假 为真
为真 p则
p则 则
则
 有下列命题:
有下列命题: 的周期为
的周期为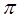 ;
;  是
是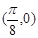 是
是 个单位,可得到
个单位,可得到 的图象.
的图象. ; p2:|a+b|>1?θ∈
; p2:|a+b|>1?θ∈
 ; p4:|a-b|>1?θ∈
; p4:|a-b|>1?θ∈ .
. ≥0”的否定是“
≥0”的否定是“ <0”
<0” ”的充分不必要条件
”的充分不必要条件