题目内容
(15分)已知命题p:方程x2+mx+1=0有负实数根;
命题q:方程4x2+4(m-2)x+1=0无实数根,
若“p或q”为真命题,“p且q”为假命题,求实数m的取值范围。
命题q:方程4x2+4(m-2)x+1=0无实数根,
若“p或q”为真命题,“p且q”为假命题,求实数m的取值范围。
1<m<2或m≥3
先根据命题p和命题q为真的情况求出m的范围,再根据真值表列出与m的不等式组,最后利用不等式知识解得m的取值范围
解:p:方程有负根m=-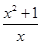 =-(x+
=-(x+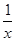 )≥2;q:方程无实数根∴1<m<3
)≥2;q:方程无实数根∴1<m<3
“p或q”为真命题,“p且q”为假命题∴p、 q一真一假∴1<m<2或m≥3
所以实数m的取值范围为1<m<2或m≥3。
解:p:方程有负根m=-
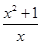 =-(x+
=-(x+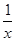 )≥2;q:方程无实数根∴1<m<3
)≥2;q:方程无实数根∴1<m<3 “p或q”为真命题,“p且q”为假命题∴p、 q一真一假∴1<m<2或m≥3
所以实数m的取值范围为1<m<2或m≥3。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,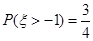 ,
,
 ;
; ”是“直线
”是“直线 与直线
与直线 相互垂直”的充要条件;
相互垂直”的充要条件; 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为 ,则
,则 ;
; 的解集为R,则
的解集为R,则
 满足
满足 ,且在[-3,-2]上是减函数,若
,且在[-3,-2]上是减函数,若 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则 与
与 的大小关系为 ;
的大小关系为 ; :“
:“ ”,命题
”,命题 :“直线
:“直线 与圆
与圆 相切”,则
相切”,则 现有下列命题:
现有下列命题:  是偶函数;
是偶函数; 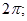
 是函数
是函数 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减. ,使
,使
 ,
, 


 ,
, 的定义域;
的定义域; 上的最小值;
上的最小值; ,命题p:关于x的不等式
,命题p:关于x的不等式 对函数
对函数 恒成立;命题q:指数函数
恒成立;命题q:指数函数 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围. ,则
,则 为:
为: .
.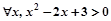 ”的否命题是“
”的否命题是“ ”.
”. 则q”的逆否命题是“若p,则
则q”的逆否命题是“若p,则 ”.
”.  ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆; 与椭圆
与椭圆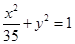 有相同的焦点;
有相同的焦点; 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; ,则点P的轨迹是一条直线.
,则点P的轨迹是一条直线.