题目内容
5.已知数列{an}的首项a1=1,且对每个n∈N*,an,an+1是方程x2+2nx+bn=0的两根,则b10=189.分析 an,an+1是方程x2+2nx+bn=0的两根,可得an+an+1=-2n,an•an+1=bn.于是an+2-an=-2.因此数列{an}的奇数项与偶数项分别成等差数列,公差都为-2,首项分别为1,-3.即可得出.
解答 解:∵an,an+1是方程x2+2nx+bn=0的两根,
∴an+an+1=-2n,an•an+1=bn.
∴an+2-an=-2.
∴数列{an}的奇数项与偶数项分别成等差数列,公差都为-2,首项分别为1,-3.
∴a2k-1=1-2(n-1)=3-2n,a2k=-3-2(k-1)=-1-2k,
∴b10=a10a11=(-1-20)×(3-12)=189.
故答案为:189.
点评 本题考查了等差数列的通项公式、递推关系的应用、一元二次方程的根与系数的关系,考查了推理能力能力与计算能力,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
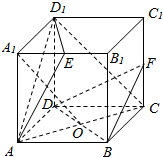 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.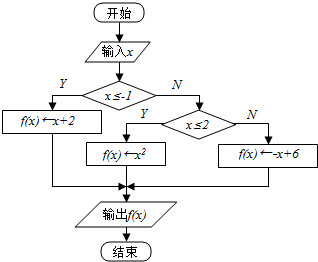 根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).
根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).