题目内容
8.给出下列关于互不相同的直线m,n,l和平面α,β的四个命题:(1)m?α,l∩α=A,点A∉m,则l与m不共面;
(2)l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;
(3)若l∥α,m∥β,α∥β,则l∥m;
(4)若l?α,m?α,l∩m=点A,l∥β,m∥β,则α∥β,
其中为错误的命题是( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据空间点线面直线的关系以及直线平行,直线和平面平行或垂直的关系进行判断即可.
解答 解:(1)若m?α,l∩α=A,点A∉m,则l与m是异面直线,则l与m不共面;正确.
(2)l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;正确.
(3)若l∥α,m∥β,α∥β,则l∥m不正确,有可能相交或者是异面直线;
(4)若l?α,m?a,l∩m=点A,l∥β,m∥β,则α∥β,正确,
故错误的是(3),
故选:A.
点评 本题主要考查空间直线和平面位置关系的判断,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.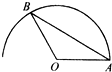 如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )
如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )
 如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )
如图所示,OA=1,在以O为圆心,OA为半径的半圆弧长任取一点B,则使△AOB的面积大于等于$\frac{1}{4}$的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
20.曲线y=$\frac{{e}^{x}}{{e}^{x}+1}$的切线斜率最大时切线方程是( )
| A. | x-4y-2=0 | B. | x+4y+2=0 | C. | x-4y+2=0 | D. | x+4y-2=0 |
18.一个正方体的八个顶点都在同一个球面上,已知这个正方体的体积是8,则这个球的表面积是( )
| A. | 4π | B. | 8π | C. | 12π | D. | 24π |