题目内容
已知函数 的定义域为R,对任意
的定义域为R,对任意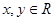 ,均有
,均有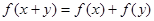 ,且对任意
,且对任意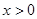 都有
都有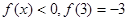 .
.
(1)试证明:函数 在R上是单调函数;
在R上是单调函数;
(2)判断 的奇偶性,并证明;
的奇偶性,并证明;
(3)解不等式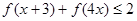 ;
;
(4)试求函数 在
在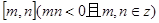 上的值域.
上的值域.
 的定义域为R,对任意
的定义域为R,对任意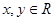 ,均有
,均有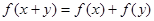 ,且对任意
,且对任意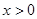 都有
都有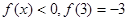 .
.(1)试证明:函数
 在R上是单调函数;
在R上是单调函数;(2)判断
 的奇偶性,并证明;
的奇偶性,并证明;(3)解不等式
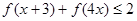 ;
;(4)试求函数
 在
在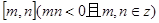 上的值域.
上的值域.解:(1)任取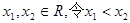
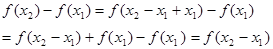 ………………2分
………………2分
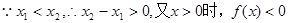
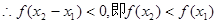
∴ 在R上是单调减函数. ……………… 4分
在R上是单调减函数. ……………… 4分
(2)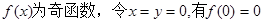 ……………… 5分
……………… 5分
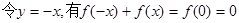
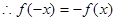 ……………… 7分
……………… 7分
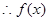 为奇函数 ……………… 8分
为奇函数 ……………… 8分
(3)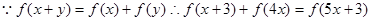
又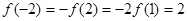 ……………… 9分
……………… 9分
∴原不等式为: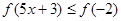 ……………… 10分
……………… 10分
∵ 在R上递减,
在R上递减,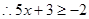
∴不等式的解集为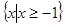 ……………… 11分
……………… 11分
(4)由题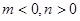
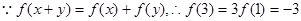
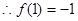
又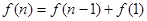
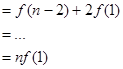
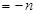 ……………… 12分
……………… 12分
由(2)知 为奇函数,
为奇函数,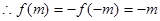 ……………… 13分
……………… 13分
由(1)知, 在
在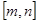 上递减,
上递减,
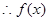 的值域为
的值域为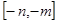 ……………… 14分
……………… 14分
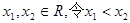
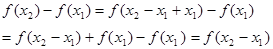 ………………2分
………………2分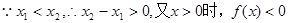
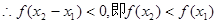
∴
 在R上是单调减函数. ……………… 4分
在R上是单调减函数. ……………… 4分(2)
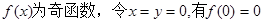 ……………… 5分
……………… 5分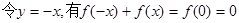
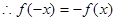 ……………… 7分
……………… 7分 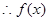 为奇函数 ……………… 8分
为奇函数 ……………… 8分(3)
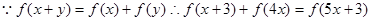
又
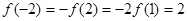 ……………… 9分
……………… 9分∴原不等式为:
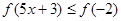 ……………… 10分
……………… 10分∵
 在R上递减,
在R上递减,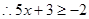
∴不等式的解集为
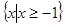 ……………… 11分
……………… 11分(4)由题
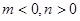
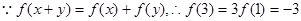
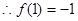
又
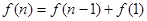
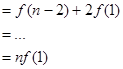
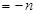 ……………… 12分
……………… 12分由(2)知
 为奇函数,
为奇函数,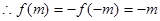 ……………… 13分
……………… 13分由(1)知,
 在
在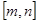 上递减,
上递减,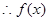 的值域为
的值域为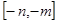 ……………… 14分
……………… 14分略

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
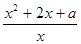 ,x
,x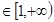 ,
,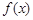 是定义在
是定义在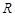 上的奇函数,且当
上的奇函数,且当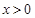 时
时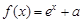 ,若
,若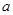 的最小值是
的最小值是 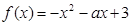 在区间
在区间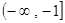 上是增函数,则实数
上是增函数,则实数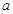 的取值范围为____________
的取值范围为____________ 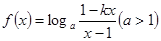 是奇函数,
是奇函数,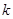 的值;
的值;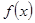 在
在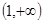 上的单调性,并运用单调性的定义予以证明.
上的单调性,并运用单调性的定义予以证明.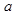 >0且
>0且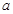 ≠1.
≠1. 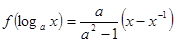
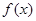 的解析式;
的解析式; 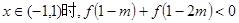 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. =0,则不等式f(log4x)>0的解集为 ( )
=0,则不等式f(log4x)>0的解集为 ( )

 在
在 上的最大值与最小值之和为3,则
上的最大值与最小值之和为3,则 的值是 。
的值是 。