题目内容
2.已知f′(x)是奇函数f(x)的导函数,f(-1)=0,当x>0时,xf′(x)-f(x)>0,则使得f(x)>0成立的x的取值范围是( )| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
分析 根据题意构造函数g(x)=$\frac{f(x)}{x}$,由求导公式和法则求出g′(x),结合条件判断出g′(x)的符号,即可得到函数g(x)的单调区间,根据f(x)奇函数判断出g(x)是偶函数,由f(-1)=0求出g(-1)=0,结合函数g(x)的单调性、奇偶性,再转化f(x)>0,由单调性求出不等式成立时x的取值范围.
解答 解:由题意设g(x)=$\frac{f(x)}{x}$,则g′(x)=$\frac{x{f}^{′}(x)-f(x)}{{x}^{2}}$
∵当x>0时,有xf′(x)-f(x)>0,
∴当x>0时,g′(x)>0,
∴函数g(x)=$\frac{f(x)}{x}$在(0,+∞)上为增函数,
∵函数f(x)是奇函数,
∴g(-x)=$\frac{f(-x)}{-x}$=$\frac{-f(x)}{-x}$=$\frac{f(x)}{x}$=g(x),
∴函数g(x)为定义域上的偶函数,
g(x)在(-∞,0)上递减,
由f(-1)=0得,g(-1)=0,
∵不等式f(x)>0?x•g(x)>0,
∴$\left\{\begin{array}{l}{x>0}\\{g(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{g(x)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{x>0}\\{g(x)>g(1)}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{g(x)<g(-1)}\end{array}\right.$,
即有x>1或-1<x<0,
∴使得f(x)>0成立的x的取值范围是:(-1,0)∪(1,+∞),
故选:B.
点评 本题考查利用导数判断函数的单调性,由函数的奇偶性、单调性解不等式,考查构造函数法,转化思想和数形结合思想,属于综合题.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案| A. | $\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{DB}$ | B. | $\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BO}$=$\overrightarrow{OC}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{BD}$ |
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | 3 |
| A. | 函数f(x)的最小正周期为2π | B. | 函数f(x)在区间$[0,\frac{π}{2}]$上单调递增 | ||
| C. | 函数f(x)的图象关于y轴对称 | D. | 点(π,0)是函数f(x)的一个对称中心 |
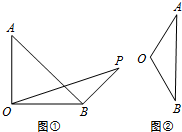 在△AOB中,OA=OB=2,
在△AOB中,OA=OB=2, 将数列{an}按如图所示的规律排成一个三角形表,并同时满足以下两个条件:
将数列{an}按如图所示的规律排成一个三角形表,并同时满足以下两个条件: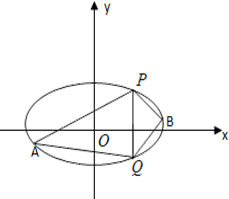 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.