题目内容
已知函数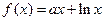
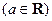 .
.
(Ⅰ)求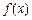 的单调区间;
的单调区间;
(Ⅱ)设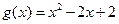 ,若对任意
,若对任意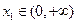 ,均存在
,均存在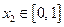 ,使得
,使得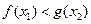 ,求
,求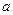 的取值范围。
的取值范围。
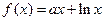
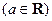 .
.(Ⅰ)求
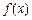 的单调区间;
的单调区间;(Ⅱ)设
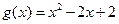 ,若对任意
,若对任意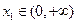 ,均存在
,均存在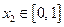 ,使得
,使得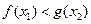 ,求
,求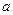 的取值范围。
的取值范围。解:(Ⅰ)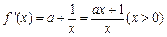 .
.
①当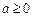 时,由于
时,由于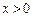 ,故
,故 ,
,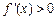
所以,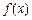 的单调递增区间为
的单调递增区间为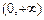
②当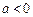 时,由
时,由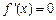 ,得
,得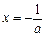 .
.
在区间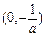 上,
上,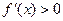 ,在区间
,在区间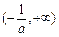 上
上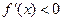 ,
,
所以,函数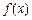 的单调递增区间为
的单调递增区间为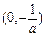 ,单调递减区间为
,单调递减区间为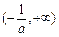 .
.
(Ⅱ)由已知,转化为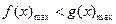 .
.
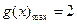
由(Ⅱ)知,当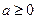 时,
时,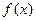 在
在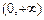 上单调递增,值域为
上单调递增,值域为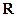 ,故不符合题意.
,故不符合题意.
(或者举出反例:存在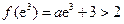 ,故不符合题意.)
,故不符合题意.)
当 时,
时,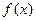 在
在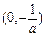 上单调递增,在
上单调递增,在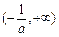 上单调递减,
上单调递减,
故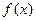 的
的 极大值即为最大值,
极大值即为最大值,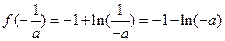 ,
,
所以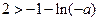 ,
,
解得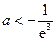 .
.
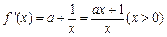 .
.①当
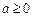 时,由于
时,由于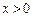 ,故
,故 ,
,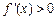
所以,
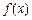 的单调递增区间为
的单调递增区间为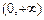
②当
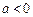 时,由
时,由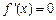 ,得
,得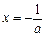 .
.在区间
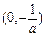 上,
上,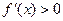 ,在区间
,在区间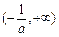 上
上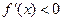 ,
,所以,函数
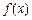 的单调递增区间为
的单调递增区间为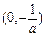 ,单调递减区间为
,单调递减区间为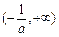 .
.(Ⅱ)由已知,转化为
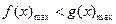 .
.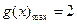
由(Ⅱ)知,当
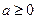 时,
时,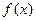 在
在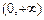 上单调递增,值域为
上单调递增,值域为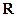 ,故不符合题意.
,故不符合题意.(或者举出反例:存在
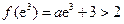 ,故不符合题意.)
,故不符合题意.)当
 时,
时,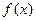 在
在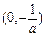 上单调递增,在
上单调递增,在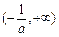 上单调递减,
上单调递减,故
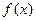 的
的 极大值即为最大值,
极大值即为最大值,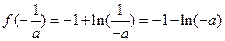 ,
,所以
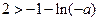 ,
,解得
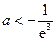 .
.略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
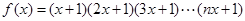 ,则
,则 ( )
( )
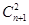
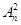

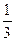 x3+
x3+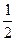 ax2+ax-2(a∈R),
ax2+ax-2(a∈R),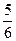 ,求实数a的取值范围.
,求实数a的取值范围. -x (e为自然对数的底数).
-x (e为自然对数的底数).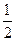 ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠ ,求实数a的
,求实数a的 =
=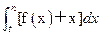 (t为常数,t≥0),是否存在等比数列{
(t为常数,t≥0),是否存在等比数列{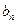 },使得b1+b2+…
},使得b1+b2+…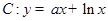 存在斜率为
存在斜率为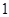 的切线,则实数
的切线,则实数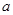 的取值范围是 .
的取值范围是 . 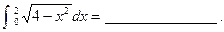
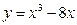 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于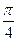 的点中,坐标为整数的点的个是
的点中,坐标为整数的点的个是 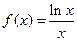 ,若
,若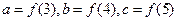 , 则
, 则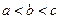
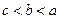
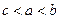
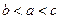
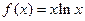 ,若
,若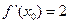 ,则
,则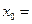 ____________.
____________.