题目内容
【题目】以原点为圆心,半径为![]() 的圆
的圆![]()
![]() 与直线
与直线![]() 相切.
相切.
(1)直线![]() 过点
过点![]() 且
且![]() 截圆
截圆![]() 所得弦长为
所得弦长为![]() 求直线
求直线![]()
![]() 的方程;
的方程;
(2)设圆![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]()
![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]()
![]() ,证明:直线
,证明:直线![]() 恒过一个定点,并求出该定点坐标.
恒过一个定点,并求出该定点坐标.

【答案】(1)![]() 或
或![]()
![]() ;(2)
;(2)![]() .
.
【解析】
分析:(1)先由直线和圆相切得到圆的方程,再由垂径定理列式,分直线斜率存在与不存在两种情况得到结果;(3)联立直线和圆,由韦达定理得到交点的坐标,由这两个点写出直线方程,进而得到直线过定点.
详解:
(1)∵圆![]() 与直线
与直线![]()
![]() 相切,
相切,
∴圆心![]() 到直线的距离为
到直线的距离为![]() ,
,
∴圆![]() 的方程为:
的方程为:![]()
若直线![]() 的斜率不存在,直线
的斜率不存在,直线![]() 为
为![]()
![]() ,
,
此时直线![]() 截圆所得弦长为
截圆所得弦长为![]()
![]() ,符合题意;
,符合题意;
若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 为
为![]()
![]() ,
,
由题意知,圆心到直线的距离为![]()
![]() ,解得:
,解得:![]() ,
,
此时直线![]() 为
为![]() ,
,
则所求的直线![]() 为
为![]() 或
或![]()
![]()
(2)由题意知,![]()
![]() ,设直线
,设直线![]() ,
,
与圆方程联立得:![]()
![]() ,
,
消去![]() 得:
得:![]()
![]() ,
,
∴![]() ∴
∴![]() ,
,![]()
用![]() 换掉
换掉![]() 得到B点坐标
得到B点坐标
∴![]() ,
,![]()
![]()
∴直线AB的方程为![]()
整理得:![]()
则直线AB恒过定点为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】中国共产党第十九次全国代表大会于2017年10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚“情况,从某县调查得到农村居民2011年至2017年家庭人均纯收入![]() (单位:百元)的数据如下表:
(单位:百元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 41 | 45 | 48 | 56 | 60 | 64 | 71 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入能否达到“全面建成小康社会”的标准?
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
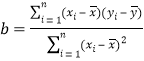 ,
,![]()
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.

