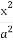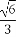题目内容
已知圆O1的方程为x2+(y+1)2=6,圆O2的圆心坐标为(2,1).若两圆相交于A,B两点,且|AB|=4,求圆O2的方程.
(x-2)2+(y-1)2=6或(x-2)2+(y-1)2=22
【解析】设圆O2的方程为(x-2)2+(y-1)2=r2(r>0).
∵圆O1的方程为x2+(y+1)2=6,
∴直线AB的方程为4x+4y+r2-10=0.
圆心O1到直线AB的距离d=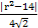 ,
,
由d2+22=6,得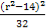 =2,
=2,
∴r2-14=±8,r2=6或22.
故圆O2的方程为(x-2)2+(y-1)2=6或(x-2)2+(y-1)2=22.
【方法技巧】求解相交弦问题的技巧
把两个圆的方程进行相减得:x2+y2+D1x+E1y+F1-(x2+y2+D2x+E2y+F2)=0即(D1-D2)x+(E1-E2)y+(F1-F2)=0 ①
我们把直线方程①称为两圆C1,C2的根轴,
当两圆C1,C2相交时,方程①表示两圆公共弦所在的直线方程;
当两圆C1,C2相切时,方程①表示过圆C1,C2切点的公切线方程.

练习册系列答案
相关题目