题目内容
已知0<k<4,直线l1:kx-2y-2k+8=0和直线l2:2x+k2y-4k2-4=0与两坐标轴围成一个四边形,则使得这个四边形面积最小的k值为 .
【解析】由题意知直线l1,l2恒过定点P(2,4),直线l1的纵截距为4-k,直线l2的横截距为2k2+2,如图所示:
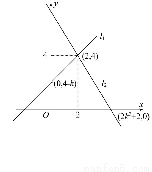
所以四边形的面积S=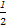 [(4-k)+4]×2+
[(4-k)+4]×2+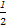 ×4×[(2k2+2)-2]=4k2-k+8,故面积最小时,k=
×4×[(2k2+2)-2]=4k2-k+8,故面积最小时,k=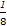 .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
题目内容
已知0<k<4,直线l1:kx-2y-2k+8=0和直线l2:2x+k2y-4k2-4=0与两坐标轴围成一个四边形,则使得这个四边形面积最小的k值为 .
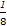
【解析】由题意知直线l1,l2恒过定点P(2,4),直线l1的纵截距为4-k,直线l2的横截距为2k2+2,如图所示:

所以四边形的面积S=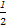 [(4-k)+4]×2+
[(4-k)+4]×2+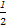 ×4×[(2k2+2)-2]=4k2-k+8,故面积最小时,k=
×4×[(2k2+2)-2]=4k2-k+8,故面积最小时,k=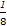 .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案