题目内容
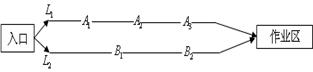
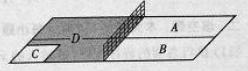
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有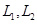 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图),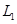 巷道有
巷道有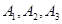 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是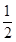 ;
;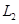 巷道有
巷道有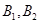 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为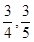 .
.
(1)求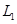 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若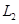 巷道中堵塞点个数为
巷道中堵塞点个数为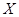 ,求
,求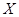 的分布列及数学期望
的分布列及数学期望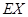 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
(1)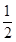 ;(2)分布列详见解析;
;(2)分布列详见解析; ;选择
;选择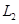 巷道为抢险路线为好.
巷道为抢险路线为好.
解析试题分析:(1)利用互独立事件的概率计算公式即可得出; 为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
(2)写出随机变量X的所有可能取值,然后计算相应的概率,列表即得分布列,由数学期望公式计算期望的大小.
比较走两条路的数学期望的大小,即可得出要选择的路线.
(1)设 巷道中,三个易堵塞点最多有一个被堵塞
巷道中,三个易堵塞点最多有一个被堵塞 为事件
为事件
则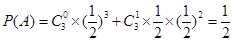 4分
4分
(2)依题意,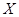 的可能取值为0,1,2
的可能取值为0,1,2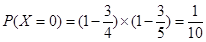
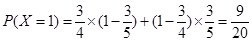
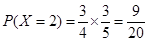
所以,随机变量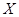 的分布列为:
的分布列为: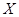
0 1 2 
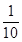
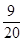
 8分
8分
(方法一)设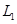 巷道中堵塞点个数为
巷道中堵塞点个数为 ,则
,则 的可能取值为0,1,2,3
的可能取值为0,1,2,3
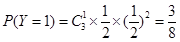
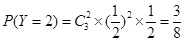
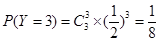
所以,随机变量 的分布列为:
的分布列为:
0 1 2 3 

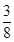
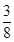


1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
喜爱打篮球
不喜爱打篮球
合计
男生
5
女生
10
合计
50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .(12分)
.(12分)
(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为 ,求
,求 的分布列与期望.
的分布列与期望.
下面的临界值表供参考:
0.15
0.10
0.05[
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式: ,其中
,其中 )
)
 甲上有两个不相交的区域
甲上有两个不相交的区域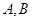 ,乙被划分为两个不相交的区域
,乙被划分为两个不相交的区域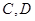 .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在
.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在 上记3分,在
上记3分,在 上记1分,其它情况记0分.对落点在
上记1分,其它情况记0分.对落点在 上的来球,队员小明回球的落点在
上的来球,队员小明回球的落点在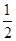 ,在
,在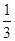 ;对落点在
;对落点在 上的来球,小明回球的落点在
上的来球,小明回球的落点在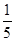 ,在
,在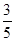 .假设共有两次来球且落在
.假设共有两次来球且落在 的分布列与数学期望.
的分布列与数学期望.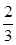 ,乙获胜的概率为
,乙获胜的概率为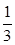 ,各局比赛结果相互独立.
,各局比赛结果相互独立.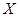 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求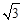 的圆形靶内有一个半径为
的圆形靶内有一个半径为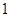 的同心圆,将大圆分成两
的同心圆,将大圆分成两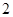 环,圆环区域记为
环,圆环区域记为 枚飞镖,每次
枚飞镖,每次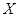 表示该同学在
表示该同学在
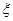 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求
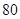 分的次数为
分的次数为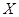 ,求
,求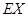 ..
..