题目内容
在△ABC中,|
|=4,|
|=2,D是BC边上一点,
=
+
.
(1)求证:∠BAD=∠CAD;
(2)若|
|=
,求|
|的值.

| AB |
| AC |
| AD |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
(1)求证:∠BAD=∠CAD;
(2)若|
| AD |
| 6 |
| BC |

证明:(1)设
=
,
则
=
-
=
+
-
即
=
,
又∵|
|=4,
∴|
|=
,|
|=
•2=
,
又由ED∥AC,
可得∠BAD=∠EDA=∠CAD
(2)由|
|=
得
6=|
|2=(
+
)2=
•16+
•
+
•4⇒
•
=
,
则|
|2=(
-
)2=4-2
•
+16=9⇒
=3
| AE |
| 1 |
| 3 |
| AB |
则
| ED |
| AD |
| AE |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| AB |
即
| ED |
| 2 |
| 3 |
| AC |
又∵|
| AB |
∴|
| AE |
| 4 |
| 3 |
| ED |
| 2 |
| 3 |
| 4 |
| 3 |
又由ED∥AC,
可得∠BAD=∠EDA=∠CAD
(2)由|
| AD |
| 6 |
6=|
| AD |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
| 1 |
| 9 |
| 4 |
| 9 |
| AB |
| AC |
| 4 |
| 9 |
| AB |
| AC |
| 11 |
| 2 |
则|
| BC |
| AC |
| AB |
| AC |
| AB |
| BC |

练习册系列答案
相关题目
 ,
, ,
, ,
, .当
.当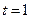 ,
, ,
, ,
, 时,分别求点
时,分别求点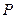 的坐标.
的坐标.
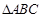 中,
中,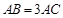 ,
,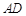 是
是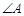 的平分线,且
的平分线,且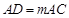 ,则实数
,则实数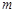 的取值范围是 ▲ .
的取值范围是 ▲ . 为椭圆
为椭圆 的左、右焦点,
的左、右焦点, 是椭圆上一点。
是椭圆上一点。 的最大值;
的最大值; 且
且 的面积为
的面积为 ,求
,求 的值;
的值;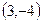 与圆
与圆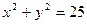 相切的直线方程是 .
相切的直线方程是 .