题目内容
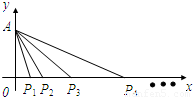 在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*.
在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn,且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn,n∈N*.(1)若
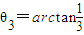 ,求点A的坐标;
,求点A的坐标;(2)若点A的坐标为(0,8
 ),求θn的最大值及相应n的值.
),求θn的最大值及相应n的值.
【答案】分析:(1)利用{xn} 是首项为1、公比为2的等比数列,确定通项,利用差角的正切公式,建立方程,即可求得A的坐标;
(2)表示出tanθn=tan(∠OAPn+1-∠OAPn),利用基本不等式,结合正切函数的单调性,即可求得结论.
解答:解:(1)设A(0,t)(t>0),根据题意,xn=2n-1.
由 ,知
,知 ,
,
而tanθ3=tan(∠OAP4-∠OAP3)= =
= ,
,
所以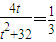 ,解得t=4或t=8.
,解得t=4或t=8.
故点A的坐标为(0,4)或(0,8).
(2)由题意,点Pn的坐标为(2n-1,0),tan∠OAPn= .
.
∴tanθn=tan(∠OAPn+1-∠OAPn)= =
= .
.
因为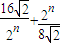 ≥
≥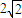 ,所以tanθn≤
,所以tanθn≤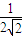 =
= ,
,
当且仅当 ,即n=4时等号成立.
,即n=4时等号成立.
∵0<θn< ,y=tanx在(0,
,y=tanx在(0,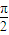 )上为增函数,
)上为增函数,
∴当n=4时,θn最大,其最大值为 .
.
点评:本题考查等比数列,考查差角的正切函数,考查基本不等式的运用,正确运用差角的正切公式是关键.
(2)表示出tanθn=tan(∠OAPn+1-∠OAPn),利用基本不等式,结合正切函数的单调性,即可求得结论.
解答:解:(1)设A(0,t)(t>0),根据题意,xn=2n-1.
由
 ,知
,知 ,
,而tanθ3=tan(∠OAP4-∠OAP3)=
 =
= ,
,所以
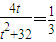 ,解得t=4或t=8.
,解得t=4或t=8.故点A的坐标为(0,4)或(0,8).
(2)由题意,点Pn的坐标为(2n-1,0),tan∠OAPn=
 .
.∴tanθn=tan(∠OAPn+1-∠OAPn)=
 =
= .
.因为
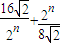 ≥
≥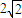 ,所以tanθn≤
,所以tanθn≤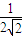 =
= ,
,当且仅当
 ,即n=4时等号成立.
,即n=4时等号成立.∵0<θn<
 ,y=tanx在(0,
,y=tanx在(0,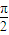 )上为增函数,
)上为增函数,∴当n=4时,θn最大,其最大值为
 .
.点评:本题考查等比数列,考查差角的正切函数,考查基本不等式的运用,正确运用差角的正切公式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是