Question

【题目】物业公司为了改善某小区空气质量和居住环境，计划将小区内部的空地种植绿植，平时许多用户将私家车停在空地上，为了了解该小区居民对种植绿植的态度，在该小区中随机抽查了100人进行了调查，调查情况如下表：

年龄段
频数	5	15	20		20	10
赞成人数	3	12	17	18	16	2

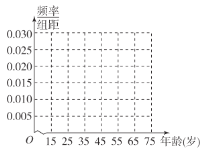
（1）求出表格中的值，并完成被调查人员年龄的频率分布图．

（2）若从年龄在被调查者中按照是否赞成进行分层抽样，从中抽取5人参与某项调查，然后再从这5人中随机抽取2人参加座谈会，求选出的2人中至少有1人赞成“种植绿植”的概率．

Answer 1

【答案】（1），见解析（2）

【解析】

（1）由样本容量求出的值，填写频率分布表，即可画出频率分布直方图；

（2）由（1）知，年龄在的共有30人，其中赞成的有18人，不赞成的有12人，利用分层抽样求出抽取的5人中赞成者人数为3人，不赞成人数为2人，一一列出基本事件，根据古典概型即可求出概率.

解：（1）由题知被调查者一共100人，

所以有，

解得：，

则被调查人员年龄各组的频率为，，，，，，

所以频率分布表如下：

年龄段
频数	5	15	20	30	20	10
频率	0.05	0.15	0.20	0.30	0.20	0.10
频率/组距	0.005	0.015	0.020	0.030	0.020	0.010

所以被调查人员年龄的频率分布直方图如下图所示：

（2）由（1）知，年龄在的共有30人，其中赞成的有18人，不赞成的有12人，

由分层抽样赞成者应选人，记为，，；不赞成有2人，记为，，

从中选取2人，不同的取法有：，，，，，

，，，，，共10种，

其中至少有1人赞成的取法有：，，，，，

，，，，共9种，

故选出的2人中至少有1人赞成“种植绿植”的概率为．