题目内容
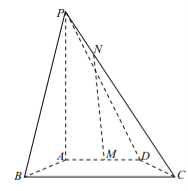
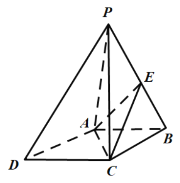
【题目】在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() 是
是![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)设![]() 是直线
是直线![]() 上的动点,当点
上的动点,当点![]() 到平面
到平面![]() 距离最大时,求面
距离最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,根据菱形的性质,结合线面垂直的判定定理和性质进行证明即可;
,根据菱形的性质,结合线面垂直的判定定理和性质进行证明即可;
(2)根据面面垂直的判定定理和性质定理,可以确定点![]() 到直线
到直线![]() 的距离即为点
的距离即为点![]() 到平面
到平面![]() 的距离,结合垂线段的性质可以确定点
的距离,结合垂线段的性质可以确定点![]() 到平面
到平面![]() 的距离最大,最大值为1.
的距离最大,最大值为1.
以![]() 为坐标原点,直线
为坐标原点,直线![]() 分别为
分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .利用空间向量夹角公式,结合同角的三角函数关系式进行求解即可.
.利用空间向量夹角公式,结合同角的三角函数关系式进行求解即可.
(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,
,
因为四边形![]() 为菱形且
为菱形且![]() .
.
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() .
.
同理可证![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:由(1)得![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
所以点![]() 到直线
到直线![]() 的距离即为点
的距离即为点![]() 到平面
到平面![]() 的距离.
的距离.
过![]() 作
作![]() 的垂线段,在所有的垂线段中长度最大的为
的垂线段,在所有的垂线段中长度最大的为![]() ,此时
,此时![]() 必过
必过![]() 的中点,
的中点,
因为![]() 为
为![]() 中点,所以此时,点
中点,所以此时,点![]() 到平面
到平面![]() 的距离最大,最大值为1.
的距离最大,最大值为1.
以![]() 为坐标原点,直线
为坐标原点,直线![]() 分别为
分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
则![]()
所以![]()
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则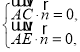 即
即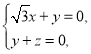
取![]() ,则
,则![]() ,
,
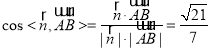 ,
,
所以![]() ,
,
所以面![]() 与面
与面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】物业公司为了改善某小区空气质量和居住环境,计划将小区内部的空地种植绿植,平时许多用户将私家车停在空地上,为了了解该小区居民对种植绿植的态度,在该小区中随机抽查了100人进行了调查,调查情况如下表:
年龄段 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 |
| 20 | 10 |
赞成人数 | 3 | 12 | 17 | 18 | 16 | 2 |
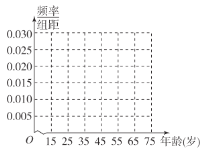
(1)求出表格中![]() 的值,并完成被调查人员年龄的频率分布图.
的值,并完成被调查人员年龄的频率分布图.
(2)若从年龄在![]() 被调查者中按照是否赞成进行分层抽样,从中抽取5人参与某项调查,然后再从这5人中随机抽取2人参加座谈会,求选出的2人中至少有1人赞成“种植绿植”的概率.
被调查者中按照是否赞成进行分层抽样,从中抽取5人参与某项调查,然后再从这5人中随机抽取2人参加座谈会,求选出的2人中至少有1人赞成“种植绿植”的概率.
【题目】新高考取消文理科,实行“![]() ”模式,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人,并把调查结果制成下表:
”模式,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人,并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)把年龄在![]() 称为中青年,年龄在
称为中青年,年龄在![]() 称为中老年,请根据上表完成
称为中老年,请根据上表完成![]() 列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
了解新高考 | 不了解新高考 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
附: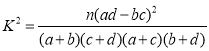 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)若从年龄在![]() 的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为
的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.