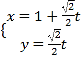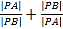题目内容
【题目】己知动点![]() 在圆
在圆![]() 上,则
上,则![]() 的取值范围是____________,若点
的取值范围是____________,若点![]() ,点
,点![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
【答案】![]()
![]()
【解析】
(1)令![]() ,则所求问题转化为求圆上任意一点到
,则所求问题转化为求圆上任意一点到![]() 的斜率范围,数形结合确定边界即可求解;
的斜率范围,数形结合确定边界即可求解;
(2)分析![]() 特点可知,两线段前的系数并不统一,如果要转化成最值问题,需将
特点可知,两线段前的系数并不统一,如果要转化成最值问题,需将![]() 转化,画出图像,结合相似三角形,可得
转化,画出图像,结合相似三角形,可得![]() ,点
,点![]() 为
为![]() ,则所求问题转化为求
,则所求问题转化为求![]() 距离最值,当点
距离最值,当点![]() 在
在![]() 连线与圆的交点上时,有最小值
连线与圆的交点上时,有最小值
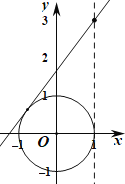
(1)如图,令![]() ,所求问题等价于求圆上动点与
,所求问题等价于求圆上动点与![]() 连线的斜率范围,当斜线斜率不存在时,相切于右边界,当直线斜率存在时,若相切于第二象限,设直线方程为
连线的斜率范围,当斜线斜率不存在时,相切于右边界,当直线斜率存在时,若相切于第二象限,设直线方程为![]() ,则
,则![]() ,解得
,解得![]() ,则
,则![]() 的取值范围是
的取值范围是![]() ;
;
(2)
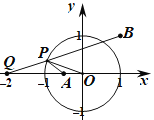
如图所示,当![]() 在
在![]() 轴上时,
轴上时,![]() ,
,![]() ,
,
![]() ;
;
当![]() 不在
不在![]() 轴上时,
轴上时,![]() ,作点
,作点![]() 为
为![]() ,则有
,则有![]() ,则
,则![]() ,则有
,则有![]() ,即
,即![]() ,则
,则![]() ,当点
,当点![]() 在
在![]() 连线与圆的交点上时,有最小值
连线与圆的交点上时,有最小值![]() ;
;
综上所述,![]() 的最小值为
的最小值为![]()
故答案为:![]() ;
;![]()

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案【题目】为了了解手机品牌的选择是否和年龄的大小有关,随机抽取部分华为手机使用者和苹果机使用者进行统计,统计结果如下表:
年龄 手机品牌 | 华为 | 苹果 | 合计 |
30岁以上 | 40 | 20 | 60 |
30岁以下(含30岁) | 15 | 25 | 40 |
合计 | 55 | 45 | 100 |
附:
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根据表格计算得![]() 的观测值
的观测值![]() ,据此判断下列结论正确的是( )
,据此判断下列结论正确的是( )
A.没有任何把握认为“手机品牌的选择与年龄大小有关”
B.可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”
C.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”
D.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小无关”
【题目】某省积极响应教育部号召实行新课程改革,为了调查某校高三学生的物理考试成绩是否达到![]() 级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
考试成绩达到 | 考试成绩未达到 | 总计 | |
男生 | 26 | 40 | |
女生 | 6 | ||
总计 | 70 |
(1)(ⅰ)将![]() 列联表补充完整;
列联表补充完整;
(ⅱ)据此列联表判断,能否有![]() 的把握认为“物理考试成绩是否达到级与性别有关”?
的把握认为“物理考试成绩是否达到级与性别有关”?
(2)将频率视作概率,从该校高三年级任意抽取3名学生的成绩,求物理考试成绩达到![]() 级的人数的分布列及期望.
级的人数的分布列及期望.
附: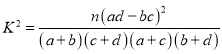
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10..828 |
【题目】物业公司为了改善某小区空气质量和居住环境,计划将小区内部的空地种植绿植,平时许多用户将私家车停在空地上,为了了解该小区居民对种植绿植的态度,在该小区中随机抽查了100人进行了调查,调查情况如下表:
年龄段 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 |
| 20 | 10 |
赞成人数 | 3 | 12 | 17 | 18 | 16 | 2 |
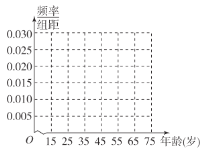
(1)求出表格中![]() 的值,并完成被调查人员年龄的频率分布图.
的值,并完成被调查人员年龄的频率分布图.
(2)若从年龄在![]() 被调查者中按照是否赞成进行分层抽样,从中抽取5人参与某项调查,然后再从这5人中随机抽取2人参加座谈会,求选出的2人中至少有1人赞成“种植绿植”的概率.
被调查者中按照是否赞成进行分层抽样,从中抽取5人参与某项调查,然后再从这5人中随机抽取2人参加座谈会,求选出的2人中至少有1人赞成“种植绿植”的概率.