题目内容
2．已知：log0.2x（x+2）≥log0.23，求x的取值范围．分析 由对数函数的单调性化对数不等式为一元二次不等式组求解．
解答 解：由log0.2x（x+2）≥log0.23，得$\left\{\begin{array}{l}{x（x+2）＞0}\\{x（x+2）≤3}\end{array}\right.$，
解得：-3≤x＜-2或0＜x≤1．
∴不等式log0.2x（x+2）≥log0.23的解集为[-3，-2）∪（0，1]．
点评 本题考查对数不等式的解法，考查了对数函数的性质，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．直线ax-y-1=0与直线（2a+3）x-ay+1=0平行，则a=（ ）
| A． | 3 | B． | -1 | C． | -1或3 | D． | -1或3或0 |
17．某单位招聘职工分为笔试和面试两个环节，将笔试成绩合格（满分100分，及格60分，精确到个位数）的应聘者进行统计，得到如下的频率分布表：
（I）确定表中a，b，x，y的值（直接写出结果，不必写过程）
（Ⅱ）面试规定，笔试成绩在80分（不含80分）以上者可以进入面试环节，面试时又要分两关，首先面试官依次提出4个问题供选手回答，并规定，答对2道题就终止回答，通过第一关可以进入下一关，如果前三题均没有答对，则不再回答第四题并且不能进入下一关，假定某选手获得面试资格的概率与答对每道题的概率相等．
①求该选手答完3道题而通过第一关的概率；
②记该选手在面试第一关中的答题个数为X，求X的分布列及数学期望．
| 分组 | 频数 | 频率 |
| [60，70] | a | 0.16 |
| （70，80] | 22 | x |
| （80，90] | 14 | 0.28 |
| （90，100] | b | y |
| 合计 | 50 | 1 |
（Ⅱ）面试规定，笔试成绩在80分（不含80分）以上者可以进入面试环节，面试时又要分两关，首先面试官依次提出4个问题供选手回答，并规定，答对2道题就终止回答，通过第一关可以进入下一关，如果前三题均没有答对，则不再回答第四题并且不能进入下一关，假定某选手获得面试资格的概率与答对每道题的概率相等．
①求该选手答完3道题而通过第一关的概率；
②记该选手在面试第一关中的答题个数为X，求X的分布列及数学期望．
7．函数y=3sin（$\frac{x}{2}$-$\frac{π}{8}$）的振幅、周期、初相分别为（ ）
| A． | -3，4π，$\frac{π}{8}$ | B． | 3，4π，-$\frac{π}{8}$ | C． | 3，π，-$\frac{π}{8}$ | D． | -3，π，$\frac{π}{8}$ |
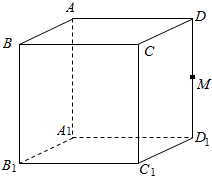如图，M是正方体ABCD-A1B1C1D1的棱DD1的中点，给出下列命题：