题目内容
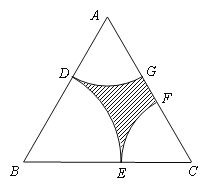
【题目】近年来,随着我市经济的快速发展,政府对民生也越来越关注. 市区现有一块近似正三角形土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中![]() 、
、![]() 与
与![]() 分别相切于点D、E,且
分别相切于点D、E,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出最大面积.
【答案】(1) ![]() (2) 当BD长为
(2) 当BD长为![]() 百米时,草坪面积最大,最大值为(
百米时,草坪面积最大,最大值为(![]() )百米2.
)百米2.
【解析】试题分析:(1)根据扇形面积公式可得结果,根据条件可得![]() ,且BD长小于高,解得x的取值范围;(2)列出草坪面积函数关系式,根据二次函数对称轴与定义区间位置关系求最值
,且BD长小于高,解得x的取值范围;(2)列出草坪面积函数关系式,根据二次函数对称轴与定义区间位置关系求最值
试题解析:(1)如图, ![]() ,则
,则![]() ,
, ![]() ,
,
在扇形![]() 中,弧
中,弧![]() 长=
长= ![]() ,
,
所以![]() ,
,
同理, ![]() ,
,
因为弧DG与弧EF无重叠,
所以![]() ,即
,即![]() ,则
,则![]() ,
,
又三个扇形都在三角形内部,则![]() ,
,
所以![]() .
.
(2)因为![]() ,
,
所以![]() =
=![]()
=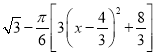 ,
,
所以当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ,
,
答:当BD长为![]() 百米时,草坪面积最大,最大值为(
百米时,草坪面积最大,最大值为(![]() )百米2.
)百米2.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下: 表1:男生表2:女生
等级 | 优秀 | 合格 | 尚待改进 | 等级 | 优秀 | 合格 | 尚待改进 | |
频数 | 15 | x | 5 | 频数 | 15 | 3 | y |
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
参考数据与公式:
K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2>k0) | 0.05 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了50名女性和50名男性,根据调研结果得到如图所示的等高条形图
(Ⅰ)完成下列2×2列联表:
喜欢旅游 | 不喜欢旅游 | 合计 | |
女性 | |||
男性 | |||
合计 |
(II)能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关”
附:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)

