题目内容
用0,1,2,3,4这五个数字组成无重复数字的自然数。
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数。
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数。
(Ⅰ)共有30个符合题意的三位偶数。
(Ⅱ)共有20个符合题意的“凹数
(Ⅲ)共有28个符合题意的五位数
(Ⅱ)共有20个符合题意的“凹数
(Ⅲ)共有28个符合题意的五位数
本试题主要是考查了排列组合在实际生活中的运用。
(1)将所有的三位偶数分为两类,个位数是0,个位数是2,或者4.来讨论得到。
(2)将这些“凹数”分为三类:
若十位数字为0,则共有12(种);若十位数字为1,则共有6(种); 若十位数字为2,则共有2(种)
(3)将符合题意的五位数分为三类:
若两个奇数数字在一、三位置,则共有12(种);
若两个奇数数字在二、四位置,则共有8(种);
若两个奇数数字在三、五位置,则共有种得到结论。
解:(Ⅰ)将所有的三位偶数分为两类:
(1)若个位数为0,则共有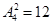 (种); 1分
(种); 1分
(2)若个位数为2或4,则共有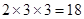 (种) 2分
(种) 2分
所以,共有30个符合题意的三位偶数。 3分
(Ⅱ)将这些“凹数”分为三类:
(1)若十位数字为0,则共有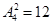 (种); 4分
(种); 4分
(2)若十位数字为1,则共有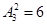 (种); 5分
(种); 5分
(3)若十位数字为2,则共有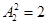 (种),
(种),
所以,共有20个符合题意的“凹数” 6分
(Ⅲ)将符合题意的五位数分为三类:
(1)若两个奇数数字在一、三位置,则共有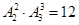 (种); 7分
(种); 7分
(2)若两个奇数数字在二、四位置,则共有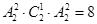 (种); 8分
(种); 8分
(3)若两个奇数数字在三、五位置,则共有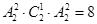 (种),
(种),
所以,共有28个符合题意的五位数。 9分
(1)将所有的三位偶数分为两类,个位数是0,个位数是2,或者4.来讨论得到。
(2)将这些“凹数”分为三类:
若十位数字为0,则共有12(种);若十位数字为1,则共有6(种); 若十位数字为2,则共有2(种)
(3)将符合题意的五位数分为三类:
若两个奇数数字在一、三位置,则共有12(种);
若两个奇数数字在二、四位置,则共有8(种);
若两个奇数数字在三、五位置,则共有种得到结论。
解:(Ⅰ)将所有的三位偶数分为两类:
(1)若个位数为0,则共有
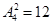 (种); 1分
(种); 1分(2)若个位数为2或4,则共有
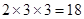 (种) 2分
(种) 2分所以,共有30个符合题意的三位偶数。 3分
(Ⅱ)将这些“凹数”分为三类:
(1)若十位数字为0,则共有
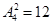 (种); 4分
(种); 4分(2)若十位数字为1,则共有
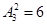 (种); 5分
(种); 5分(3)若十位数字为2,则共有
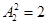 (种),
(种),所以,共有20个符合题意的“凹数” 6分
(Ⅲ)将符合题意的五位数分为三类:
(1)若两个奇数数字在一、三位置,则共有
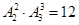 (种); 7分
(种); 7分(2)若两个奇数数字在二、四位置,则共有
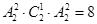 (种); 8分
(种); 8分(3)若两个奇数数字在三、五位置,则共有
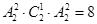 (种),
(种),所以,共有28个符合题意的五位数。 9分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
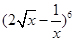 的展开式中常数项的系数为_____________.
的展开式中常数项的系数为_____________.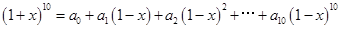 ,则
,则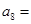 ( )
( )