题目内容
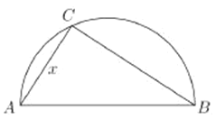
【题目】如图，以
，
为顶点作正三角形
，再以
和
的中点
为顶点作正三角形
，再以
和
的中点
为顶点作正三角形
，
，如此继续下去.有如下结论：
①所作的正三角形的边长构成公比为
的等比数列；
②每一个正三角形都有一个顶点在直线
上；
③第六个正三角形的不在第五个正三角形边上的顶点
的坐标是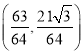
；
④第
个正三角形的不在第
个正三角形边上的顶点
的横坐标是
，则
.
其中正确结论的序号是___________.（把你认为正确结论的序号都填上）
【答案】①②③④
【解析】
根据规律可判断①②真假，结合图形求出点
的坐标，可判断③真假，求出第
个正三角形的不在第
个正三角形边上的顶点
的横坐标是
，然后求极限可得结论.
解：由题意可得，每一个正三角形的边长都是上一个正三角形边长的
，故①正确；
根据图形的规律可知每一个正三角形都有一个顶点在直线
上，故②正确；
第六个正三角形的边长为
，故顶点的横坐标为
，
的纵坐标为
，从而顶点的纵坐标为
，故③正确；
第个正三角形的不在第
个正三角形边上的顶点的横坐标是，
，
，
，
，
，通过图象可得
，故④正确.
故答案为：①②③④.
练习册系列答案
相关题目
