Question

若an＝n2＋λn＋3(其中λ为实常数)，n∈N*，且数列{an}为单调递增数列，则实数λ的取值范围为________．

 

Answer 1

(－3，＋∞)

【解析】解法1：(函数观点)因为{an}为单调递增数列，所以an＋1＞an，即(n＋1)2＋λ(n＋1)＋3＞n2＋λn＋3，化简为λ＞－2n－1对一切n∈N*都成立，所以λ＞－3.

故实数λ的取值范围为(－3，＋∞)．

解法2：(数形结合法)因为{an}为单调递增数列，所以a1＜a2，要保证a1＜a2成立，二次函数f(x)＝x2＋λx＋3的对称轴x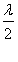＝－应位于1和2中点的左侧，即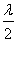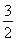－＜，亦即λ＞－3，故实数λ的取值范围为(－3，＋∞)．