题目内容
15.已知函数y=$\frac{2kx-8}{{k}^{2}{x}^{2}+3kx+1}$的定义域为R,求实数k的值.分析 把函数y=$\frac{2kx-8}{{k}^{2}{x}^{2}+3kx+1}$的定义域为R转化为对任意实数x,k2x2+3kx+1≠0恒成立,然后分k=0和k≠0分类求解.
解答 解:∵函数y=$\frac{2kx-8}{{k}^{2}{x}^{2}+3kx+1}$的定义域为R,
∴对任意实数x,k2x2+3kx+1≠0恒成立,
若k=0,则k2x2+3kx+1≠0恒成立;
若k≠0,
∵△=9k2-4k2=5k2≥0恒成立,∴k2x2+3kx+1≠0不成立.
∴k=0.
点评 本题考查函数的定义域及其求法,考查了分类讨论的数学思想方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若A={x|x<1},B={x|x2+2x>0},则A∩B=( )
| A. | (0,1) | B. | (-∞,-2) | C. | (-2,0) | D. | (-∞,-2)∪(0,1) |
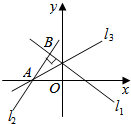 如果直线l1的倾斜角是150°,l2⊥l1,垂足为B,l1,l2与x轴分别相交于点C,A,l3平分∠BAC,则l3的倾斜角为30°.
如果直线l1的倾斜角是150°,l2⊥l1,垂足为B,l1,l2与x轴分别相交于点C,A,l3平分∠BAC,则l3的倾斜角为30°.