题目内容
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 是矩形,且平面
是矩形,且平面![]() 平面
平面![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求这个六面体
,求这个六面体![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】
(1)由![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,由面面垂直的性质可得结果;(2)以
,由面面垂直的性质可得结果;(2)以![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立平面直角坐标系,设
轴建立平面直角坐标系,设![]() ,利用向量垂直数量积为零列方程求出平面
,利用向量垂直数量积为零列方程求出平面![]() 的一个法向量与平面
的一个法向量与平面![]() 的一个法向量,利用空间向量夹角余弦公式,列方程可求得
的一个法向量,利用空间向量夹角余弦公式,列方程可求得![]() ,由棱锥的体积公式可得结果.
,由棱锥的体积公式可得结果.
(Ⅰ)在梯形![]() 中,∵
中,∵![]() ,
,![]() ,
,
 ∴
∴![]()
![]() ,
,
∴![]()
![]() ,∵
,∵![]() .
.
∴![]()
![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)在![]() 中,
中,![]()
![]()
![]() ,∴
,∴![]() .
.
分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立平面直角坐标系, 设
轴建立平面直角坐标系, 设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,则
,则![]() ,
,![]() ,易知平面
,易知平面![]() 的一个法向量为
的一个法向量为![]() ,设
,设
∵平面![]() 的法向量为
的法向量为![]() ,∴
,∴ 即
即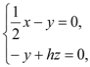 令
令![]() ,则
,则![]() ,
,![]() ,
,
∴平面![]() 的法向量为
的法向量为![]() ,∵二面角
,∵二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,
,
∴![]()
![]()
![]() ,解得
,解得![]() ,即
,即![]() .
.
所以六面体![]() 的体积为:
的体积为:
![]()
![]()
![]()
![]()
![]()
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】“微信运动”是一个类似计步数据库的公众账号,现从“微信运动”的![]() 个好友(男、女各
个好友(男、女各![]() 人)中,记录了他们某一天的走路步数,并将数据整理如下表:
人)中,记录了他们某一天的走路步数,并将数据整理如下表:
0-2000步 | 2001-5000步 | 5001-8000步 | 8001-10000步 | >10000步 | |
男(人数) | 2 | 4 | 6 | 10 | 8 |
女(人数) | 1 | 7 | 10 | 9 | 3 |
(1)若某人一天的走路步数超过![]() 步被系统评定为“积极型”,否则评定为“懈怠型",根据题意完成下面的
步被系统评定为“积极型”,否则评定为“懈怠型",根据题意完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() %的把握认为“评定类型"与“性别“有关?
%的把握认为“评定类型"与“性别“有关?
积极型 | 懈怠型 | 总计 | |
男(人数) | |||
女(人数) | |||
总计 |
(2)现从被系统评定为“积极型”好友中,按男女性别分层抽样,共抽出![]() 人,再从这
人,再从这![]() 人中,任意抽出
人中,任意抽出![]() 人发一等奖,求发到一等奖的
人发一等奖,求发到一等奖的![]() 中恰有一名女性的概率.
中恰有一名女性的概率.
附: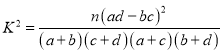
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |