题目内容
3.化简:$\sqrt{\frac{1-sinθ}{1+sinθ}}$+$\sqrt{\frac{1+sinθ}{1-sinθ}}$($\frac{3π}{2}$<θ<2π)分析 根据$\frac{3π}{2}$<θ<2π,可得:sinθ∈(-1,0),cosθ∈(0,1),进而根据同角三角函数的基本关系,及$\sqrt{{a}^{2}}=\left|a\right|$对原式进行化简.
解答 解:∵$\frac{3π}{2}$<θ<2π,
∴sinθ∈(-1,0),cosθ∈(0,1),
∴$\sqrt{\frac{1-sinθ}{1+sinθ}}$+$\sqrt{\frac{1+sinθ}{1-sinθ}}$=$\sqrt{\frac{(1-sinθ)^{2}}{(1+sinθ)(1-sinθ)}}$+$\sqrt{\frac{{(1+sinθ)}^{2}}{(1+sinθ)(1-sinθ)}}$=$\sqrt{\frac{{(1-sinθ)}^{2}}{{cos}^{2}θ}}$+$\sqrt{\frac{{(1+sinθ)}^{2}}{{cos}^{2}θ}}$=$\left|\frac{1-sinθ}{cosθ}\right|$+$\left|\frac{1+sinθ}{cosθ}\right|$=$\frac{1-sinθ}{cosθ}$+$\frac{1+sinθ}{cosθ}$=$\frac{2}{cosθ}$
点评 本题考查的知识点是三角函数的化简与求值,难度不大,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
14.在△ABC中,已知a,b,c分别为∠A,∠B,∠C所对的边,且a=4$\sqrt{3}$,b=4,∠A=60°,则∠B=( )
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
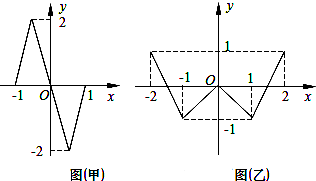 奇函数f(x)与偶函数g(x)的图象分别如图甲与图乙所示,设方程f(g(x))=0与g(f(x))=0的实根个数分别为a,b,则a+b的值为14.
奇函数f(x)与偶函数g(x)的图象分别如图甲与图乙所示,设方程f(g(x))=0与g(f(x))=0的实根个数分别为a,b,则a+b的值为14.