题目内容

【题目】如图，已知正方体ABCD－A1B1C1D1的棱长为3，M，N分别是棱AA1，AB上的点，且AM＝AN＝1.

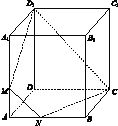
（1）证明：M，N，C，D1四点共面；

（2）平面MNCD1将此正方体分为两部分，求这两部分的体积之比.

【答案】（1）略（2）

【解析】（1）证明：连接A1B，

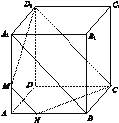
在四边形A1BCD1中，A1D1∥BC且A1D1＝BC

所以四边形A1BCD1是平行四边形

所以A1B∥D1C

在△ABA1中，AM＝AN＝1，AA1＝AB＝3，

所以，

所以MN∥A1B

所以MN∥D1C

所以M，N，C，D1四点共面.

（2）记平面MNCD1将正方体分成两部分的下部分体积为V1，上部分体积为V2，连接D1A，D1N，DN，则几何体D1－AMN，D1－ADN，D1－CDN均为三棱锥，

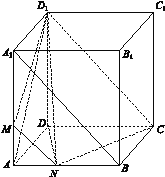
所以V1＝

＝S△AMN·D1A1＋S△ADN·D1D＋S△CDN·D1D

＝××3＋××3＋××3

＝.

从而V2＝－V1＝27－＝，所以，

所以平面MNCD1分此正方体的两部分体积的比为.

练习册系列答案
相关题目

【题目】下列说法中正确的是__________．

①一个命题的逆命题为真，则它的逆否命题一定为真；

②“”是“”的充要条件；

③“，则， 全为” 的逆否命题是“若， 全不为，则”

④一个命题的否命题为真，则它的逆命题一定为真；

⑤“为假命题”是“为真命题”的充分不必要条件．

【题目】已知函数.

(Ⅰ)试求函数的单调区间；

(Ⅱ)若不等式对任意的恒成立，求实数的取值范围.

【题目】如图所示，在△ABC中，a＝b·cos C＋c·cos B，其中a，b，c分别为角A，B，C的对边，在四面体PABC中，S1，S2，S3，S分别表示△PAB，△PBC，△PCA，△ABC的面积，α，β，γ依次表示面PAB，面PBC，面PCA与底面ABC所成二面角的大小．写出对四面体性质的猜想，并证明你的结论

【题目】一个圆柱形圆木的底面半径为1 m，长为10 m，将此圆木沿轴所在的平面剖成两部分．现要把其中一部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD（如图所示，其中O为圆心，C，D在半圆上），设，木梁的体积为V（单位：m3），表面积为S（单位：m2）．

（1）求V关于θ的函数表达式；

（2）求的值，使体积V最大；

（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．

【题目】在平面直角坐标系中，已知任意角以坐标原点为顶点，轴的非负半轴为始边，若终边经过点，且，定义：，称“”为“正余弦函数”，对于“正余弦函数”，有同学得到以下性质：

①该函数的值域为； ②该函数的图象关于原点对称；

③该函数的图象关于直线对称； ④该函数为周期函数，且最小正周期为；

⑤该函数的递增区间为.

其中正确的是__________．（填上所有正确性质的序号）

【题目】已知函数 (为实常数) ．

（I）当时，求函数在上的最大值及相应的值；

（II）当时，讨论方程根的个数．

（III）若，且对任意的，都有，求

实数a的取值范围．

【题目】如图,四边形中, = == 分别在上, ,现将四边形沿折起,使.

(1)若,在折叠后的线段上是否存在一点,使得平面?若存在,求出的值;若不存在,说明理由;

(2)求三棱锥的体积的最大值,并求出此时点到平面的距离.

【题目】一个棱锥的三视图如图,则该棱锥的全面积为(　 )

A. B.

C. D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网