题目内容
【题目】正整数数列![]() 的前
的前![]() 项和为
项和为![]() ,前
,前![]() 项积
项积![]() ,若
,若![]() ,则称数列
,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)判断下列数列是否是![]() 数列,并说明理由;①2,2,4,8;②8,24,40,56
数列,并说明理由;①2,2,4,8;②8,24,40,56
(2)若数列![]() 是
是![]() 数列,且
数列,且![]() .求
.求![]() 和
和![]() ;
;
(3)是否存在等差数列是![]() 数列?请阐述理由.
数列?请阐述理由.
【答案】(1) ①是;②不是;理由见解析;(2)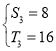 或
或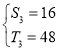 ;(3)存在.
;(3)存在.
【解析】
(1)根据新定义的![]() 数列,需要满足
数列,需要满足![]() ,所以分别计算两个数列的
,所以分别计算两个数列的![]() ,
,![]() ,相比观察得答案;
,相比观察得答案;
(2)由![]() 数列的定义可知
数列的定义可知![]() ,分别表示
,分别表示![]() ,由正整数数列可分别求得
,由正整数数列可分别求得![]() ,即得
,即得![]() ,从而得答案;
,从而得答案;
(3) 假设存在这样的等差数列是![]() 数列,且此数列是特殊的常数列,则至少三项,分别表示所以
数列,且此数列是特殊的常数列,则至少三项,分别表示所以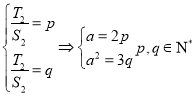 ,所以a是2和3的公倍数,令
,所以a是2和3的公倍数,令![]() ,显然该等差数列是Z数列,所以存在;此后类比推理,可到n项.
,显然该等差数列是Z数列,所以存在;此后类比推理,可到n项.
(1) ①由题可知,此时有
| 1 | 2 | 3 | 4 |
| 2 |
|
|
|
| 2 |
|
|
|
| 1 | 1 | 2 | 8 |
该数列满足![]() ,所以是
,所以是![]() 数列;
数列;
②同理可得:
| 1 | 2 | 3 | 4 |
| 8 |
|
|
|
| 8 |
|
|
|
| 1 | 6 |
| 3360 |
该数列中![]() ,所以不是
,所以不是![]() 数列.
数列.
(2) 因为数列![]() 是
是![]() 数列,
数列,
那么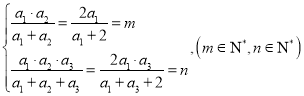 ,则
,则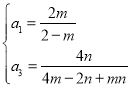
又因为数列![]() 是正整数数列,
是正整数数列,
若![]() ,则
,则![]() ,
,
所以![]() ,则
,则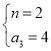 或
或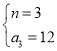
当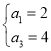 时,
时,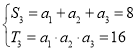 ;同理当
;同理当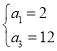 时,
时,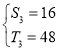
故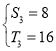 或
或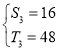
(3) )假设:存在这样的等差数列是![]() 数列,且此数列是特殊的常数列,则至少三项
数列,且此数列是特殊的常数列,则至少三项
所以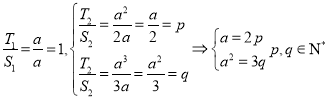 ,所以a是2和3的公倍数
,所以a是2和3的公倍数
令![]() ,显然该等差数列是Z数列,所以存在;
,显然该等差数列是Z数列,所以存在;
同理,如果是四项,则需满足每项是2,3,4的公倍数,如12,12,12,12
如此类推的有限等差数列,可以有无穷多个,且当为n项时,则各项为![]() 的公倍数
的公倍数
故存在等差数列是![]() 数列.
数列.

【题目】某届奥运会上,中国队以26金18银26铜的成绩列金牌榜第三奖牌榜第二.某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了60人,具体的调查结果如下表:
班号 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
频数 | 6 | 10 | 13 | 11 | 9 | 11 |
满意人数 | 5 | 9 | 10 | 6 | 7 | 7 |
(1)在高三年级全体学生中随机抽取1名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班和二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.