Question

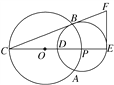
【题目】如图，圆O与圆P相交于A，B两点，圆心P在圆O上，圆O的弦BC切圆P于点B，CP及其延长线交圆P于D，E两点，过点E作EF⊥CE，交CB的延长线于点F.

(1)求证：B，P，E，F四点共圆；

(2)若CD＝2，CB＝2 ，求出由B，P，E，F四点所确定的圆的直径．

Answer 1

【答案】(1)见解析(2)

【解析】试题分析：（1）欲证四点B、P、E、F共圆，只要通过三角形Rt△CBP和Rt△CEF相似证明由此四点构成的四边形对角互补即可；

（2）先根据（1）中四点B，P，E，F共圆条件得切线，再由切割线定理及三角形相似求得EF，最后再结合勾股定理求得PF即为所求圆的直径即可．

试题解析：

(1)证明：如图，连接PB.

因为BC切圆P于点B，所以PB⊥BC.

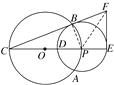因为EF⊥CE，所以∠PBF＋∠PEF＝180°，

所以B，P，E，F四点共圆．

(2)连接PF，因为B，P，E，F四点共圆，

且EF⊥CE，PB⊥BC，所以此圆的直径就是PF.

因为BC切圆P于点B，且CD＝2，CB＝2，

所以由切割线定理得CB2＝CD·CE，

所以CE＝4，所以DE＝2，则BP＝PE＝1.

又因为Rt△CBP ∽Rt△CEF，

所以＝，得EF＝.

在Rt△FEP中，PF＝＝，

即由B，P，E，F四点确定的圆的直径为.