题目内容
设平面三点A(1,0),B(0,1),C(2,5).
(1)试求向量2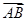 +
+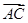 的模;
的模;
(2)试求向量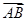 与
与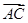 的夹角;
的夹角;
(3)试求与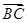 垂直的单位向量的坐标.
垂直的单位向量的坐标.
(1)试求向量2
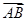 +
+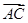 的模;
的模;(2)试求向量
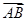 与
与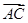 的夹角;
的夹角;(3)试求与
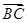 垂直的单位向量的坐标.
垂直的单位向量的坐标.(1) (2)
(2) ,
, 或(
或(
 )
)
 (2)
(2) ,
, 或(
或(
 )
)试题分析:(1)∵
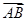 =(0-1,1-0)=(-1,1),
=(0-1,1-0)=(-1,1),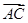 =(2-1,5-0)=(1,5).
=(2-1,5-0)=(1,5).∴2
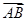 +
+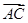 =2(-1,1)+(1,5)=(-1,7).
=2(-1,1)+(1,5)=(-1,7).∴|2
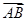 +
+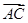 |=
|= =
= .
.(2)∵|
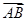 |=
|= =
= .|
.|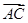 |=
|= =
= ,
,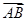 ·
·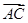 =(-1)×1+1×5=4.
=(-1)×1+1×5=4.∴cos ?=
 =
= =
= .
.(3)设所求向量为
 =(x,y),则x2+y2=1. ①
=(x,y),则x2+y2=1. ①又
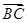 =(2-0,5-1)=(2,4),由
=(2-0,5-1)=(2,4),由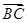 ⊥
⊥ ,得2 x +4 y =0. ②
,得2 x +4 y =0. ②由①、②,得
 或
或 ∴
∴  ,
, )或(
)或( ,
, )即为所求.
)即为所求.考点1、平面向量的模;2、平面向量的数量积;3、单位向量;4、两向量垂直的条件

练习册系列答案
相关题目
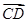
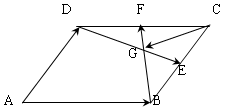
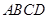 中,
中,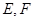 分别是
分别是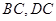 的中点,
的中点,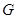 为交点,若
为交点,若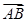 =
=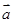 ,
,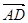 =
=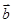 ,
, 、
、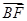 、
、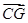 .
.
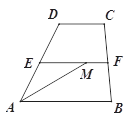
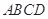 中,
中,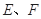 分别是腰
分别是腰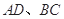 的中点,
的中点,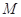 在线段
在线段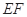 上,且
上,且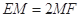 ,下底是上底的2倍,若
,下底是上底的2倍,若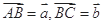 ,用
,用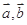 表示
表示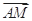 .
.
 中,已知
中,已知 ,
, ,则
,则 的值是 .
的值是 .
 与向量a=(2,3)同向,且|
与向量a=(2,3)同向,且|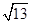 ,则点B的坐标为( )
,则点B的坐标为( )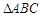 中,
中,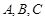 的对边分别是
的对边分别是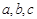 ,已知
,已知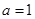 ,平面向量
,平面向量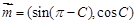 ,
,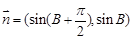 ,且
,且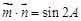 .
.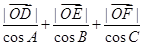 的值.
的值.