题目内容
(本小题满分14分)
已知数列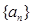 满足:
满足: ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)求数列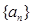 的通项
的通项 ;
;
(2)设 ,
, ,求证:
,求证: ,
,  .
.
已知数列
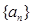 满足:
满足: ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).(1)求数列
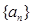 的通项
的通项 ;
;(2)设
 ,
, ,求证:
,求证: ,
,  .
.解:(1)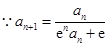 ,
,
 ,即
,即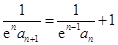 . …………………………………3分
. …………………………………3分
令 ,则
,则 ,
,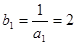 ,
,
因此,数列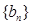 是首项为
是首项为 ,公差为
,公差为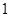 的等差数列.
的等差数列.
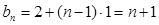 , …………………………………5分
, …………………………………5分
 . …………………………………6分
. …………………………………6分
(2)(方法一)先证明当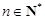 时,
时, .
.
设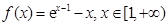 ,则
,则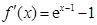 ,
,
 当
当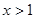 时,
时,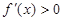 ,
,
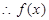 在
在 上是增函数,则当
上是增函数,则当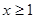 时,
时,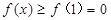 ,即
,即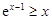 .………8分
.………8分
因此,当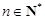 时,
时, ,
, , …………9分
, …………9分
当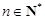 时,
时, ,
,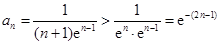 . …………………10分
. …………………10分
 .
.
…………………………12分
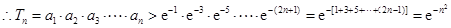 .
.
………………………14分
(方法二)数学归纳法证明
(1)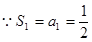 ,
,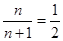 ,
, 当
当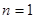 时,
时,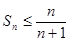 成立;
成立;
 ,
, ,
,
又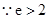 ,
,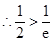 ,
,
 当
当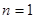 时,
时, 成立. ……………………………………………8分
成立. ……………………………………………8分
(2)设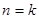 时命题成立,即
时命题成立,即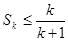 ,
,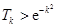 ,
,
当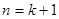 时,
时, ,
,
要证 , 即证
, 即证 ,
,
化简,即证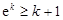 . …………………………9分
. …………………………9分
设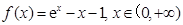 ,则
,则 ,
,
 当
当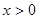 时,
时,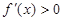 ,
,
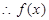 在
在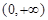 上是增函数,则当
上是增函数,则当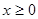 时,
时,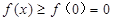 ,即
,即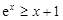 .
.
因此,不等式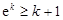 成立,即当
成立,即当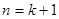 时
时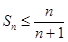 成立. …………………11分
成立. …………………11分
当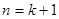 时,
时,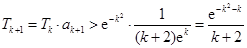 ,
,
要证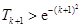 , 即证
, 即证 ,
,
化简,即证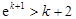 .
.
根据前面的证明,不等式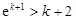 成立,则
成立,则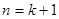 时
时 成立.
成立.
由数学归纳法可知,当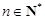 时,不等式
时,不等式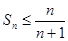 ,
, 成立.……………14分
成立.……………14分
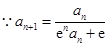 ,
, ,即
,即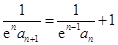 . …………………………………3分
. …………………………………3分令
 ,则
,则 ,
,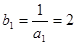 ,
,因此,数列
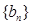 是首项为
是首项为 ,公差为
,公差为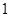 的等差数列.
的等差数列.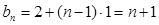 , …………………………………5分
, …………………………………5分 . …………………………………6分
. …………………………………6分(2)(方法一)先证明当
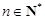 时,
时, .
.设
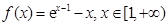 ,则
,则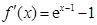 ,
, 当
当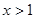 时,
时,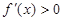 ,
,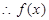 在
在 上是增函数,则当
上是增函数,则当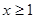 时,
时,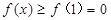 ,即
,即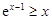 .………8分
.………8分因此,当
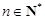 时,
时, ,
, , …………9分
, …………9分当
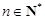 时,
时, ,
,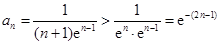 . …………………10分
. …………………10分 .
.…………………………12分
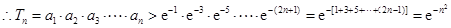 .
.………………………14分
(方法二)数学归纳法证明
(1)
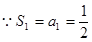 ,
,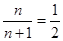 ,
, 当
当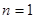 时,
时,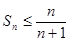 成立;
成立; ,
, ,
,又
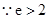 ,
,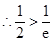 ,
, 当
当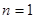 时,
时, 成立. ……………………………………………8分
成立. ……………………………………………8分(2)设
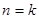 时命题成立,即
时命题成立,即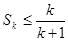 ,
,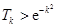 ,
,当
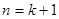 时,
时, ,
,要证
 , 即证
, 即证 ,
,化简,即证
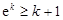 . …………………………9分
. …………………………9分设
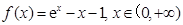 ,则
,则 ,
, 当
当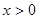 时,
时,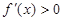 ,
,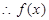 在
在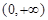 上是增函数,则当
上是增函数,则当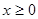 时,
时,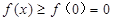 ,即
,即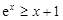 .
.因此,不等式
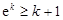 成立,即当
成立,即当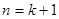 时
时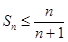 成立. …………………11分
成立. …………………11分当
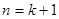 时,
时,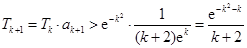 ,
,要证
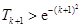 , 即证
, 即证 ,
,化简,即证
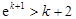 .
. 根据前面的证明,不等式
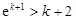 成立,则
成立,则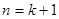 时
时 成立.
成立.由数学归纳法可知,当
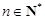 时,不等式
时,不等式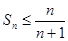 ,
, 成立.……………14分
成立.……………14分略

练习册系列答案
相关题目
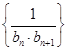 的前n项和Tn.
的前n项和Tn.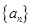 满足
满足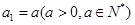 ,
,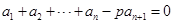
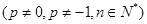 .
.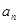 ;
;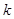 ,若将
,若将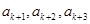 按从小到大的顺序排列后,此三项均能构成等
按从小到大的顺序排列后,此三项均能构成等 .①求
.①求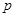 的值及对应的数列
的值及对应的数列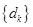 .
.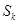 为数列
为数列 ,使得
,使得 对任意正整数
对任意正整数 中,
中, 且
且 (
( )。
)。 ,
, 的值;
的值; ,是否存在实数
,是否存在实数 ,使数列
,使数列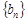 为等差数列,若存在请求其通项
为等差数列,若存在请求其通项 ,若不存在请说明理由。
,若不存在请说明理由。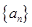 满足
满足 ,则
,则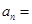 ( )
( )

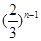

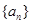 的首项
的首项
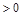 ,
,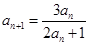 ,
,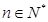
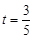 ,求证
,求证 是等比数列并求出
是等比数列并求出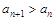 对一切
对一切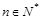 都成立,求
都成立,求 的取值范围。
的取值范围。 Sn-1 (n≥2),则Sn= .
Sn-1 (n≥2),则Sn= .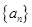 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,有
,有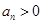 且
且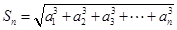 成立.
成立.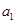 、
、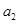 的值;
的值;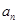 ;
;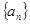 的前
的前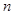 项和为
项和为 ,令
,令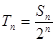 ,若对一切正整数
,若对一切正整数 ,求
,求 的取值范围.
的取值范围.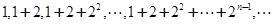 的前
的前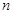 项和
项和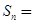 ____________.
____________.