题目内容
4.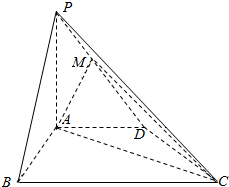 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.(1)求证:平面AMC⊥平面PAB;
(2)求四面体P-MAB的体积.
分析 (1)以A为原点,过A作BC的垂线为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法得到$\overrightarrow{AP}$⊥$\overrightarrow{AC}$,$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,由此能证明平面AMC⊥平面PAB.
(2)求出M到平面PAB的距离,利用三棱锥的体积公式,即可求四面体P-MAB的体积.
解答 (1)证明:以A为原点,过A作BC的垂线为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,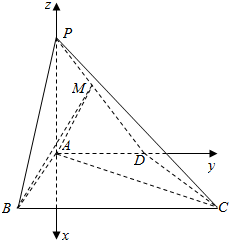
由已知得A(0,0,0),P(0,0,4),B($\sqrt{3}$,-1,0),C($\sqrt{3}$,3,0),
∴$\overrightarrow{AP}$=(0,0,4),$\overrightarrow{AB}$=($\sqrt{3},-1,0$),$\overrightarrow{AC}$=($\sqrt{3}$,3,0),
∴$\overrightarrow{AP}$•$\overrightarrow{AC}$=0,$\overrightarrow{AB}$•$\overrightarrow{AC}$=3-3+0=0,
∴$\overrightarrow{AP}$⊥$\overrightarrow{AC}$,$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,∴AP⊥AC,AB⊥AC,
∵AB∩AP=P,∴AC⊥平面PAB,
∵AC?平面AMC,∴平面AMC⊥平面PAB.
(2)解:设D到平面PAB的距离为ADsin60°=$\sqrt{3}$,
∴M到平面PAB的距离为$\frac{\sqrt{3}}{2}$.
∴四面体P-MAB的体积V=$\frac{1}{3}•\frac{1}{2}AB•PA•\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查面面垂直的证明,考查四面体P-MAB的体积,是中档题,正确运用向量法是关键.

 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | (-∞,0] | B. | (-∞,2) | C. | [0,+∞) | D. | (2,+∞) |
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2$\sqrt{2}$,∠PAB=60°.
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2$\sqrt{2}$,∠PAB=60°. 如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.
如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.