题目内容
2.求下列各式的值:(1)sin(-$\frac{11π}{6}$)+cos$\frac{12}{5}$π•tan4π;
(2)sin810°+tan1125°+cos420°;
(3)cos$\frac{25π}{3}$+tan(-$\frac{15π}{4}$);
(4)a2sin(-1350°)+b2tan405°-2abcos(-1080°)
分析 由已知条件利用三角函数的诱导公式直接求解即可.
解答 解:(1)sin(-$\frac{11π}{6}$)+cos$\frac{12}{5}$π•tan4π
=sin(-2π+$\frac{π}{6}$)+cos$\frac{12π}{5}•0$
=sin$\frac{π}{6}$
=$\frac{1}{2}$.
(2)sin810°+tan1125°+cos420°
=sin90°+tan45°+cos60°
=1+1+$\frac{1}{2}$
=$\frac{5}{2}$.
(3)cos$\frac{25π}{3}$+tan(-$\frac{15π}{4}$)
=cos$\frac{π}{3}$+tan$\frac{π}{4}$
=$\frac{1}{2}+1$
=$\frac{3}{2}$.
(4)a2sin(-1350°)+b2tan405°-2abcos(-1080°)
=-a2sin270°+b2tan45°-2abcos0°
=a2+b2-2ab
=(a-b)2.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意三角函数诱导公式的合理运用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
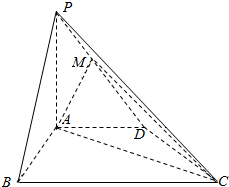 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.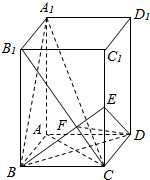 如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F.
如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F.