题目内容
16.直线l是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右准线,以原点O为圆心且过双曲线焦点的圆被直线l分成弧长为2:1的两段,则双曲线的离心率为( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
分析 根据圆被分成的两段圆弧的弧长比为2:1,可以求出两个交点与圆心构成的圆心角为120°,根据对称性,在第一象限的交点A原点O所构成直线的倾斜角为60°,求得a和c的关系,进而求得离心率e.
解答  解:如图,易求圆O的方程为:x2+y2=c2,∠AOB=120°,
解:如图,易求圆O的方程为:x2+y2=c2,∠AOB=120°,
∴A的坐标$(\frac{a^2}{c},\frac{{\sqrt{3}{a^2}}}{c})$,
∴$\frac{a^4}{c^2}+\frac{{3{a^4}}}{c^2}={c^2}⇒e=\frac{c}{a}=\sqrt{2}$,
故选:D.
点评 本题主要考查了双曲线的简单性质.考查了学生对基础知识的熟练程度.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.设F1,F2分别是椭圆x2+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<1)的左,右焦点,过F1的直线L与椭圆相交于A,B两点,|AB|=$\frac{4}{3}$,直线L的斜率为1,则b的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
8.一个球的表面积为36π,则这个球体的体积为( )
| A. | 18π | B. | 36π | C. | 72π | D. | 108π |
6.已知正实数a、b、c满足$\frac{1}{e}≤\frac{c}{a}$≤2,clnb=a+clnc,其中e是自然对数的底数,则ln$\frac{b}{a}$的取值范围是( )
| A. | [1,+∞) | B. | $[{1,\frac{1}{2}+ln2}]$ | C. | (-∞,e-1] | D. | [1,e-1] |
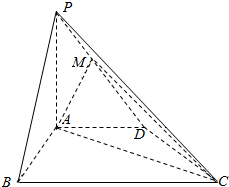 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.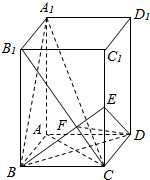 如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F.
如图,在长方形ABCD-A1B1C1D1中,AB=BC=3,BB1=4,连接B1C,过B作BE⊥B1C交CC1于E,交B1C于F. 一个空间几何体的三视图及部分数据如图所示.
一个空间几何体的三视图及部分数据如图所示.