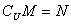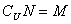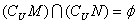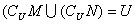题目内容
已知集合A={x|x2-2x-3≥0},B={x||x-a|<1},U=R.
(1)当a=3时,求A∩B;
(2)若A⊆∁UB,求实数a的取值范围.
(1)当a=3时,求A∩B;
(2)若A⊆∁UB,求实数a的取值范围.
(1)当a=3时,集合A={x|x2-2x-3≥0}={x|x≥3,或 x<-1},B={x||x-a|<1}={x|-1<x-3<1}={x|2<x<4},
∴A∩B={x|3≤x<4}.
(2)由题意可得CUB={x||x-a|≥1}={x|x-a≥1,或x-a≤-1}={x|x≥a+1,或x≤a-1}.
再由A⊆∁UB,可得a-1≥-1且 a+1≤3,解得0≤a≤2,即a的范围是[0,2].
∴A∩B={x|3≤x<4}.
(2)由题意可得CUB={x||x-a|≥1}={x|x-a≥1,或x-a≤-1}={x|x≥a+1,或x≤a-1}.
再由A⊆∁UB,可得a-1≥-1且 a+1≤3,解得0≤a≤2,即a的范围是[0,2].

练习册系列答案
相关题目
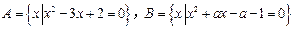 ,若
,若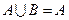 ,
,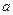 的取值。
的取值。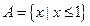 ,
, ,且
,且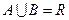 ,
,
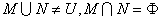 ,则下列选项中正确的是( )
,则下列选项中正确的是( )