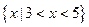题目内容
设集合A={x|x2-2x-3<0},B={x|1≤x≤4},则A∩B=( )
| A.{x|1≤x<3} | B.{x|1≤x≤3} | C.{x|3<x≤4} | D.{x|3≤x≤4} |
∵不等式x2-2x-3<0等价于(x+1)(x-3)<0
∴集合A={x|x2-2x-3<0}={x|-1<x<3},
又∵集合B={x|1≤x≤4},
∴A∩B={x|1≤x<3}.
故选A
∴集合A={x|x2-2x-3<0}={x|-1<x<3},
又∵集合B={x|1≤x≤4},
∴A∩B={x|1≤x<3}.
故选A

练习册系列答案
相关题目
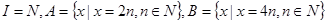 则( )
则( )



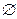
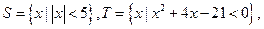 则
则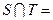 ( )
( )