题目内容
设x,y满足约束条件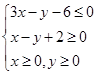 ,若目标函数z=ax+by(a>0,b>0)的最大值是12,则
,若目标函数z=ax+by(a>0,b>0)的最大值是12,则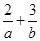 的最小值为( ).
的最小值为( ).
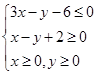 ,若目标函数z=ax+by(a>0,b>0)的最大值是12,则
,若目标函数z=ax+by(a>0,b>0)的最大值是12,则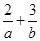 的最小值为( ).
的最小值为( ). A.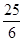 | B.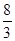 | C.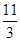 | D.4 |
A
试题分析:根据题意,由于x,y满足约束条件
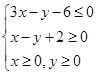 ,那么可知,目标函数z=ax+by(a>0,b>0)斜率为负数,同时当过目标区域
,那么可知,目标函数z=ax+by(a>0,b>0)斜率为负数,同时当过目标区域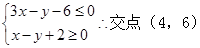 时,目标函数的截距最大,则函数值最大为12,即4a+6b=12,2a+3b=6,结合均值不等式,可知
时,目标函数的截距最大,则函数值最大为12,即4a+6b=12,2a+3b=6,结合均值不等式,可知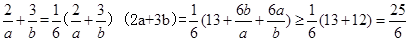 ,故选A.
,故选A.点评:解决该试题的关键是通过目标函数的最大值,来确定最优点的坐标。然后结合均值不等式求解最值,属于基础题。

练习册系列答案
相关题目
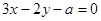 的两侧,则a的取值范围是( )
的两侧,则a的取值范围是( )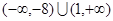
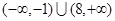
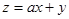 的可行域为四边形
的可行域为四边形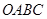 (含边界),若
(含边界),若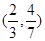 是该目标函数
是该目标函数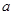 的取值范围是
的取值范围是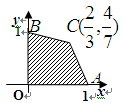
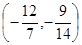
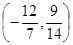
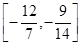
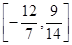
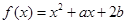 在区间(0,1)、(1,2)内各有一个零点,求
在区间(0,1)、(1,2)内各有一个零点,求 的取值范围.
的取值范围.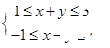 , 则
, 则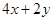 的最大值是 ;
的最大值是 ;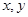 满足不等式
满足不等式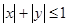 ,若
,若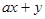 的最大值为1,则常数
的最大值为1,则常数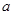 的取值范围是 。
的取值范围是 。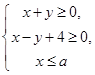 所表示的平面区域的面积是9,则实数
所表示的平面区域的面积是9,则实数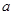 的值为 .
的值为 . 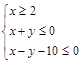 的点(x,y)形成的区域为D,区域D关于直线y=2x对称的区域为E,则区域D和区域E中距离最近的两点的距离为
的点(x,y)形成的区域为D,区域D关于直线y=2x对称的区域为E,则区域D和区域E中距离最近的两点的距离为  满足
满足 ,则
,则 的最大值为 .
的最大值为 .