题目内容
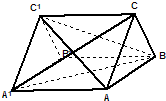
 (2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.
(2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.(1)求异面直线A1C与B1C1所成角的大小(结果用反三角函数值表示);
(2)求三棱锥C-ABC1的体积VC-ABC1.
分析:(1)连接A1B,由三棱柱的性质得C1B1∥CB,从而得到∠A1CB(或其补角)是异面直线A1C与B1C1所成角.然后在△A1CB中计算出各边的长,再根据余弦定理算出cos∠A1CB=
,即可得到异面直线A1C与B1C1所成角的大小;
(2)由棱柱体积公式,算出正三棱柱ABC-A1B1C1的体积为2
,而三棱锥C1-ABC与正三棱柱ABC-A1B1C1同底等高,得到VC1-ABC =
VABC-A1B1C1=
,由此不难得到三棱锥C-ABC1的体积VC-ABC1的值.
| ||
| 4 |
(2)由棱柱体积公式,算出正三棱柱ABC-A1B1C1的体积为2
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
解答:解:(1)连接A1B,
∵正三棱柱ABC-A1B1C1中,C1B1∥CB,
∴ ∠A1CB(或其补角)是异面直线A1C与B1C1所成角.
∠A1CB(或其补角)是异面直线A1C与B1C1所成角.
∵四边形AA1C1C与AA1B1B都是边长为2的正方形
∴|A1C|=|A1B|=2
,
△A1CB中根据余弦定理,得cos∠A1CB=
=
因此,∠A1CB=arccos
,
即异面直线A1C与B1C1所成角的大小为arccos
.
(2)由题意得
∵△ABC的面积S△ABC=
•22=
,高CC1=2
∴正三棱柱ABC-A1B1C1的体积为V=S△ABC×CC1=2
而三棱锥C1-ABC与正三棱柱ABC-A1B1C1同底等高
∴三棱锥C1-ABC的体积为VC1-ABC =
VABC-A1B1C1=
,
∵VC-ABC1=VC1-ABC ,
∴三棱锥C-ABC1的体积为
.
∵正三棱柱ABC-A1B1C1中,C1B1∥CB,
∴
 ∠A1CB(或其补角)是异面直线A1C与B1C1所成角.
∠A1CB(或其补角)是异面直线A1C与B1C1所成角.∵四边形AA1C1C与AA1B1B都是边长为2的正方形
∴|A1C|=|A1B|=2
| 2 |
△A1CB中根据余弦定理,得cos∠A1CB=
| 8+4-8 | ||
2×2
|
| ||
| 4 |
因此,∠A1CB=arccos
| ||
| 4 |
即异面直线A1C与B1C1所成角的大小为arccos
| ||
| 4 |
(2)由题意得
∵△ABC的面积S△ABC=
| ||
| 4 |
| 3 |
∴正三棱柱ABC-A1B1C1的体积为V=S△ABC×CC1=2
| 3 |
而三棱锥C1-ABC与正三棱柱ABC-A1B1C1同底等高
∴三棱锥C1-ABC的体积为VC1-ABC =
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
∵VC-ABC1=VC1-ABC ,
∴三棱锥C-ABC1的体积为
| 2 |
| 3 |
| 3 |
点评:本题给出所有棱长均相等的正三棱柱,求异面直线所成角并求三棱锥的体积,着重考查了异面直线所成角的求法和锥体、柱体体积公式等知识,属于中档题.

练习册系列答案
相关题目