题目内容
【题目】如图,甲、乙两位同学要测量河对岸A,B两点间的距离,今沿河岸选取相距40米的C,D两点,测得∠ACB=60°,∠BCD=45°,∠ADC=30°,∠CDB=90°求A,B两点间的距离. 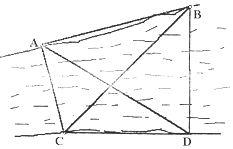
【答案】解:∵∠BDC=90°,∠BCD=45°,∴△BCD为等腰直角三角形,
又CD=40,
∴BD=CD=40,
在△ACD中,∠ACD=∠ACB+∠BCD=105°,∠ADC=30°,
∴∠CAD=45°,
又sin105°=sin(45°+60°)=sin45°cos60°+cos45°sin60°= ![]() ,
,
由正弦定理得:AD= ![]() =20(
=20( ![]() +1),
+1),
在△ABD中,利用余弦定理得:AB2=AD2+BD2﹣2ADBDcos60°=400( ![]() +1)2+402﹣800(
+1)2+402﹣800( ![]() +1)=2400,
+1)=2400,
解得:AB=20 ![]()
【解析】由∠BDC为直角,∠BCD=45°,得到三角形BCD为等腰直角三角形,可得出BD=CD=40,在三角形ACD中,利用三角形内角和定理求出∠ACD与∠CAD的度数,再由CD的长,利用正弦定理求出AD的长,在三角形ABD中,由AD,BD及cos∠ADB的值,利用余弦定理即可求出AB的长.

练习册系列答案
相关题目