题目内容
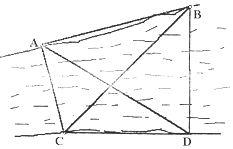
【题目】如图示：半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一
点，以AB为一边作等边三角形ABC．则四边形OACB的面积最大值是 ． 
【答案】2+ 
【解析】解：设∠AOB=α，在△AOB中，由余弦定理得：AB2=12+22﹣2×1×2cosα=5﹣4cosα，
所以四边形OACB的面积为：
S=S△AOB+S△ABC
= 
OAOBsinα+ 
AB2
= ×2×1×sinα+ （5﹣4cosα）
=sinα﹣ cosα+
=2sin（α﹣ 
）+ ，
∵0＜α＜π，
∴当α﹣ = 
，解得α= 
π，
即∠AOB= 
时，四边形OACB面积取得最大值，最大为2+ ．
【考点精析】掌握余弦定理的定义是解答本题的根本，需要知道余弦定理:
;
;
．
练习册系列答案
阅读快车系列答案
相关题目
