题目内容
8.设D、E分别是△ABC的边AB,BC上的点,AD=$\frac{1}{3}AB$,BE=$\frac{2}{3}$BC,若$\overrightarrow{DE}$=λ1$\overrightarrow{AB}$+λ2$\overrightarrow{AC}$(λ1,λ2为实数)则λ1+λ2的值为$\frac{2}{3}$.分析 利用向量共线定理、向量的三角形法则、共面向量的基本定理即可得出.
解答 解:如图所示,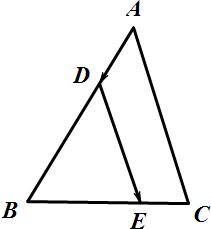
∵$\overrightarrow{DE}=\overrightarrow{DB}+\overrightarrow{BE}=\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}$=$\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}(\overrightarrow{AC}-\overrightarrow{AB})$=$0\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,
又$\overrightarrow{DE}$=λ1$\overrightarrow{AB}$+λ2$\overrightarrow{AC}$(λ1,λ2为实数)所以λ1=0,λ2=$\frac{2}{3}$,
所以λ1+λ2=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查了向量共线定理、向量的三角形法则、共面向量的基本定理,属于基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目