题目内容
12.光线从点A(-2,4)射出,经直线l:2x-y-7=0反射,反射光线过点B(5,8).(1)求入射光线所在直线方程;
(2)求光线从A到B经过的路线S.
分析 (1)求出点B关于直线l:2x-y-7=0的对称点C,则过点A,C的直线即为入射光线所在直线;
(2)直接求A,C的距离得答案.
解答 解:(1)如图,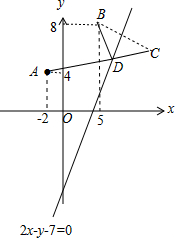
设B关于直线2x-y-7=0的对称点为C(a,b),
则$\left\{\begin{array}{l}{2•\frac{5+a}{2}-\frac{8+b}{2}-7=0}\\{\frac{b-8}{a-5}=-\frac{1}{2}}\end{array}\right.$,解得:C(9,6),
∴入射光线所在直线方程为AC所在直线方程,
由直线方程的两点式得:$\frac{y-4}{6-4}=\frac{x+2}{9+2}$,即2x-11y+48=0;
(2)光线从A到B经过的路程为|AC|=$\sqrt{(9+2)^{2}+(6-4)^{2}}=5\sqrt{5}$.
点评 本题考查求一个点关于一条直线的对称点的坐标的方法,以及用两点式求直线方程的方法,体现了数形结合的数学思想,是中档题.

练习册系列答案
相关题目
3.命题“?x∈R,3x-x3≤0”的否定是( )
| A. | ?x∈R,3x-x3≥0 | B. | ?x∈R,3x-x3>0 | C. | ?x∈R,3x-x3≥0 | D. | ?x∈R,3x-x3>0 |
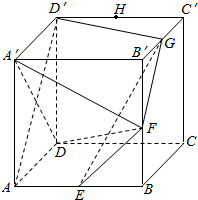 在正方体ABCD-A′B′C′D′中,棱AB、BB′、B′C′、C′D′的中点分别是E,F,G,H,如图所示,则下列说法中正确的有( )
在正方体ABCD-A′B′C′D′中,棱AB、BB′、B′C′、C′D′的中点分别是E,F,G,H,如图所示,则下列说法中正确的有( )