题目内容
17.已知点A(1,2),直线l:x=-1,两个动圆均过A且与l相切,其圆心分别为C1,C2,若满足2$\overrightarrow{{C}_{2}M}$=$\overrightarrow{{C}_{2}{C}_{1}}$+$\overrightarrow{{C}_{2}A}$,则M的轨迹方程为(y-1)2=2x-$\frac{1}{2}$.分析 由抛物线的定义可得动圆的圆心轨迹方程为y2=4x+2,利用2$\overrightarrow{{C}_{2}M}$=$\overrightarrow{{C}_{2}{C}_{1}}$+$\overrightarrow{{C}_{2}A}$,确定坐标之间的关系,即可求出M的轨迹方程.
解答 解:由抛物线的定义可得动圆的圆心轨迹方程为y2=4x+2,
设C1(a,b),C2(m,n),M(x,y),则
∵2$\overrightarrow{{C}_{2}M}$=$\overrightarrow{{C}_{2}{C}_{1}}$+$\overrightarrow{{C}_{2}A}$,
∴2(x-m,y-n)=(a-m,b-n)+(1-m,2-n),
∴2x=a+1,2y=b+2,
∴a=2x-1,b=2y-2,
∵b2=4a+2,
∴(2y-2)2=4(2x-1)+2,即(y-1)2=2x-$\frac{1}{2}$.
故答案为:(y-1)2=2x-$\frac{1}{2}$.
点评 本题考查轨迹方程,考查向量知识的运用,考查学生分析解决问题的能力,确定坐标之间的关系是关键.

练习册系列答案
相关题目
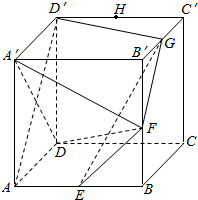 在正方体ABCD-A′B′C′D′中,棱AB、BB′、B′C′、C′D′的中点分别是E,F,G,H,如图所示,则下列说法中正确的有( )
在正方体ABCD-A′B′C′D′中,棱AB、BB′、B′C′、C′D′的中点分别是E,F,G,H,如图所示,则下列说法中正确的有( )