题目内容
已知函数 。
。
(I)求f(x)的单调区间;
(II)若对任意x∈[1,e],使得g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(III)设F(x)= ,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
 。
。(I)求f(x)的单调区间;
(II)若对任意x∈[1,e],使得g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(III)设F(x)=
 ,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。解:(Ⅰ)∵
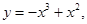
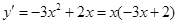
∴当
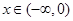 、
、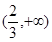 时,
时,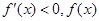 在区间
在区间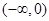 、
、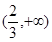 上单调递减.
上单调递减.当
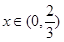 时,
时,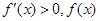 在区间
在区间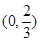 上单调递增. ………3分
上单调递增. ………3分(Ⅱ)由
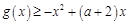 ,得
,得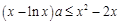 .
.∵
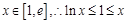 ,且等号不能同时取得,∴
,且等号不能同时取得,∴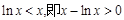 ,
,∵对任意
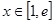 ,使得
,使得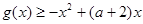 恒成立,
恒成立,∴
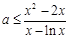 对
对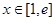 恒成立,即
恒成立,即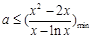 .(
.(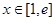 )
)令
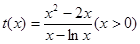 ,求导得,
,求导得,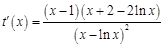 , ………5分
, ………5分∵
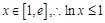 ,
,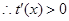
∴
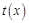 在
在 上为增函数,
上为增函数,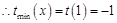 ,
, . ………7分
. ………7分(Ⅲ)由条件,
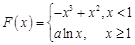 ,
,假设曲线
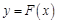 上总存在两点
上总存在两点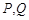 满足:
满足: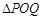 是以
是以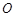 为钝角顶点的钝角三角形,且最长边的中点在
为钝角顶点的钝角三角形,且最长边的中点在 轴上,则
轴上,则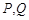 只能在
只能在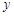 轴两侧.
轴两侧.不妨设
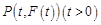 ,则
,则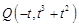 .
.∴
 ,
,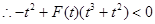 …(※),
…(※),是否存在
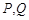 两点满足条件就等价于不等式(※)在
两点满足条件就等价于不等式(※)在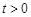 时是否有解.………9分
时是否有解.………9分① 若
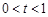 时,
时,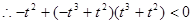 ,化简得
,化简得 ,对
,对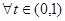 此不等式恒成立,故总存在符合要求的两点P、Q; ………11分
此不等式恒成立,故总存在符合要求的两点P、Q; ………11分② 若
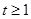 时,(※)不等式化为
时,(※)不等式化为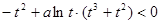 ,若
,若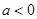 ,此不等式显然对
,此不等式显然对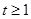 恒成立,故总存在符合要求的两点P、Q;
恒成立,故总存在符合要求的两点P、Q;若a>0时,有
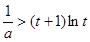 …(▲),
…(▲),设
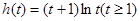 ,则
,则 ,
,显然, 当
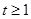 时,
时,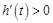 ,即
,即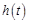 在
在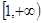 上为增函数,
上为增函数,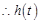 的值域为
的值域为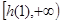 ,即
,即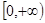 ,
, 当
当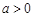 时,不等式(▲)总有解.故对
时,不等式(▲)总有解.故对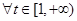 总存在符合要求的两点P、Q.
总存在符合要求的两点P、Q.………13分
综上所述,曲线
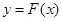 上总存在两点
上总存在两点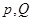 ,使得
,使得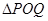 是以
是以 为钝角顶点的钝角三角形,且最长边的中点在
为钝角顶点的钝角三角形,且最长边的中点在 轴上. ………14分
轴上. ………14分略

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
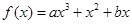 (其中常数a,b∈R)。
(其中常数a,b∈R)。 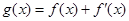 是奇函数.
是奇函数. 的表达式;
的表达式; 在区间[1,2]上的最大值和最小值.
在区间[1,2]上的最大值和最小值.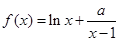 在
在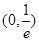 内有极值.
内有极值.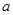 的取值范围;
的取值范围;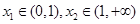 求证:
求证: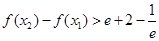 .
.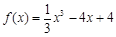 .
.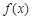 的极值;
的极值;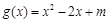 ,对
,对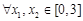 ,都有
,都有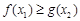 ,求实数m的取值范围.
,求实数m的取值范围.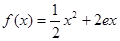 ,
,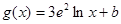 (其中
(其中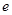 为常数,
为常数,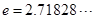 ),若这两个函数的图象有公共点,且在该点处的切线相同。
),若这两个函数的图象有公共点,且在该点处的切线相同。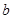 的值;
的值;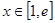 时,
时, 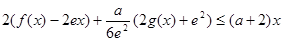 恒成立,求实数
恒成立,求实数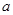 的取值范围.
的取值范围.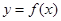 的图象如右图所示,那么导函数
的图象如右图所示,那么导函数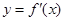 的图象可能是( )
的图象可能是( )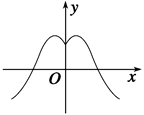
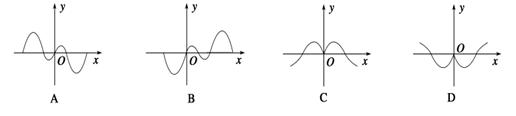
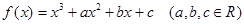 ,若函数
,若函数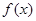 在区间
在区间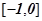 上是单调减函数,则
上是单调减函数,则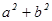 的最小值为
的最小值为
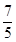


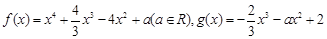 .
.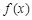 的极大值;
的极大值;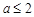 时,存在
时,存在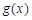 图象的上方,求实数
图象的上方,求实数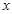 的取值范围.
的取值范围.