题目内容
已知点F(0,1),一动圆过点F且与圆x2+(y+1)2=8内切,
(1)求动圆圆心的轨迹C的方程;
(2)设点A(a,0),点P为曲线C上任一点,求点A到点P距离的最大值d(a);
(3)在0<a<1的条件下,设△POA的面积为s1(O是坐标原点,P是曲线C上横坐标为a的点),以d(a)为边长的正方形的面积为s2.若正数m满足s1≤
ms2,问m是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
(1)求动圆圆心的轨迹C的方程;
(2)设点A(a,0),点P为曲线C上任一点,求点A到点P距离的最大值d(a);
(3)在0<a<1的条件下,设△POA的面积为s1(O是坐标原点,P是曲线C上横坐标为a的点),以d(a)为边长的正方形的面积为s2.若正数m满足s1≤
| 1 | 4 |
分析:(1)设圆心坐标为P(x,y),则动圆的半径为r=
,又动圆与x2+(y+1)2=8内切,故
=|2
-r|,由此能求出动圆圆心的轨迹C的方程.
(2)设P(x,y),则|PA|2=(x-a)2+y2=(x-a)2+2-2x2=-(x+a)2+2a2+2,令f(x)=-(x+a)2+2a2+2,x∈[-1,1].再分类讨论能够推导出d(a)=
.
(3)当0<a<1时,P(a,±
),于是S1=
a
,S2=2a2+2,若正数m满足条件,则m≥
,
m2≥
,令f(a)=
,设t=a2+1,则t∈(1,2),a2=t-1,于是f(a)=
=-4(
-
)2+
,由此能够导出m存在最小值
.
| x2+(y-1)2 |
| x2+(y+1)2 |
| 2 |
(2)设P(x,y),则|PA|2=(x-a)2+y2=(x-a)2+2-2x2=-(x+a)2+2a2+2,令f(x)=-(x+a)2+2a2+2,x∈[-1,1].再分类讨论能够推导出d(a)=
|
(3)当0<a<1时,P(a,±
| 2-2a2 |
| 1 |
| 2 |
| 2(1-a2) |
a
| ||
| a2+1 |
m2≥
| 2a2(1-a2) |
| (a2+1)2 |
| 2a2(1-a2) |
| (a2+1)2 |
| 2(t-1)(2-t) |
| t2 |
| 1 |
| t |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:(1)设圆心坐标为P(x,y),则动圆的半径为r=
,
又动圆与x2+(y+1)2=8内切,
∴
=|2
-r|,
整理得2x2+y2=2,
∴动圆圆心的轨迹C的方程为2x2+y2=2.
(2)设P(x,y),则
|PA|2=(x-a)2+y2=(x-a)2+2-2x2
=-x2-2ax+a2+2
=-(x+a)2+2a2+2,
令f(x)=-(x+a)2+2a2+2,x∈[-1,1],
∴当-a<-1,即a>1时,f(x)在[-1,1]上是减函数,
[f(x)]max=f(-1)=(a+1)2.
当-1≤-a≤1,即-1≤a≤1时,f(x)在[-1,-a]上是增函数,在[-a,1]上是减函数,
则[f(x)]max=f(-a)=2a2+2.
当-a>1,即a<-1时,f(x)在[-1,1]上是增函数,
[f(x)]max=f(1)=(a-1)2,
∴d(a)=
.
(3)当0<a<1时,P(a,±
),于是S1=
a
,S2=2a2+2,
若正数m满足条件,则
a
≤
m(2a2+2),
即m≥
,
m2≥
,令f(a)=
,
设t=a2+1,则t∈(1,2),a2=t-1,
于是f(a)=
=2(
)=2(-
+
-1)=-4(
-
)2+
,
∴当
=
,即t=
∈(1,2)时,[f(a) ]max=
,
即m2≥
,m≥
,∴m存在最小值
.
| x2+(y-1)2 |
又动圆与x2+(y+1)2=8内切,
∴
| x2+(y+1)2 |
| 2 |
整理得2x2+y2=2,
∴动圆圆心的轨迹C的方程为2x2+y2=2.
(2)设P(x,y),则
|PA|2=(x-a)2+y2=(x-a)2+2-2x2
=-x2-2ax+a2+2
=-(x+a)2+2a2+2,
令f(x)=-(x+a)2+2a2+2,x∈[-1,1],
∴当-a<-1,即a>1时,f(x)在[-1,1]上是减函数,
[f(x)]max=f(-1)=(a+1)2.
当-1≤-a≤1,即-1≤a≤1时,f(x)在[-1,-a]上是增函数,在[-a,1]上是减函数,
则[f(x)]max=f(-a)=2a2+2.
当-a>1,即a<-1时,f(x)在[-1,1]上是增函数,
[f(x)]max=f(1)=(a-1)2,
∴d(a)=
|
(3)当0<a<1时,P(a,±
| 2-2a2 |
| 1 |
| 2 |
| 2(1-a2) |
若正数m满足条件,则
| 1 |
| 2 |
| 2(1-a2) |
| 1 |
| 4 |
即m≥
a
| ||
| a2+1 |
m2≥
| 2a2(1-a2) |
| (a2+1)2 |
| 2a2(1-a2) |
| (a2+1)2 |
设t=a2+1,则t∈(1,2),a2=t-1,
于是f(a)=
| 2(t-1)(2-t) |
| t2 |
| -t2+3t-2 |
| t2 |
| 2 |
| t2 |
| 3 |
| t |
| 1 |
| t |
| 3 |
| 4 |
| 1 |
| 4 |
∴当
| 1 |
| t |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 4 |
即m2≥
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
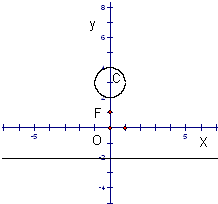 如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.
如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1. (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且