题目内容
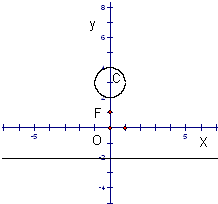 如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.
如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.(1)若动点M到点F的距离比它到直线L的距离小1,求动点M的轨迹E的方程;
(2)过点F的直线g交轨迹E于G(x1,y1)、H(x2,y2)两点,求证:x1x2 为定值;
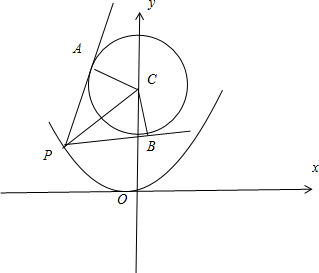
(3)过轨迹E上一点P作圆C的切线,切点为A、B,要使四边形PACB的面积S最小,求点P的坐标及S的最小值.
分析:(1)由动点M到点F的距离比它到直线L的距离小1,可得M到点F的距离与它到直y=-1的距离相等,由抛物线的定义可知M的轨迹是以F为焦点,以y=-1为准线的抛物线,从而可求方程
(2)由题意可得直线g的斜率存在,故可设直线g的方程为y=kx+1,联立直线与抛物线方程,由方程的根与系数关系可求
(3)设P(x,y),则x2=4y(y≥0),由圆的切线性质可得S四边形PACB=2S△PAC=2×
×PA×AC=PA=
=
=
,由二次函数的性质可求最小值及取得最小值时的 p
(2)由题意可得直线g的斜率存在,故可设直线g的方程为y=kx+1,联立直线与抛物线方程,由方程的根与系数关系可求
(3)设P(x,y),则x2=4y(y≥0),由圆的切线性质可得S四边形PACB=2S△PAC=2×
| 1 |
| 2 |
| PC2-1 |
| x2+(y-3)2-1 |
| y2-2y+8 |
解答:解:(1)由动点M到点F的距离比它到直线L的距离小1,可得M到点F的距离与它到直y=-1的距离相等
由抛物线的定义可知M的轨迹是以F为焦点,以y=-1为准线的抛物线
其方程为x2=4y
(2)由题意可得直线g的斜率存在,故可设直线g的方程为y=kx+1
联立方程
整理可得 x2-4kx-4=0
由方程的根与系数关系可得x1x2=-4
(3)设P(x,y),则x2=4y(y≥0)
由圆的切线的性质可得PA=PB,CA⊥PA,CB⊥PB
S四边形PACB=2S△PAC=2×
×PA×AC=PA
=
=
=
=
≥
∴P(±2,1),Smin=
由抛物线的定义可知M的轨迹是以F为焦点,以y=-1为准线的抛物线
其方程为x2=4y
(2)由题意可得直线g的斜率存在,故可设直线g的方程为y=kx+1
联立方程
|
由方程的根与系数关系可得x1x2=-4
(3)设P(x,y),则x2=4y(y≥0)
由圆的切线的性质可得PA=PB,CA⊥PA,CB⊥PB
S四边形PACB=2S△PAC=2×
| 1 |
| 2 |
=
| PC2-1 |
| x2+(y-3)2-1 |
| y2-2y+8 |
| (y-1)2+7 |
| 7 |
∴P(±2,1),Smin=
| 7 |

点评:本题主要考查了利用抛物线的定义求解抛物线的方程,方程的根与系数关系的应用,圆的切线性质的应用及利用二次函数的性质求解函数的最值等知识的综合应用.

练习册系列答案
相关题目
 (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且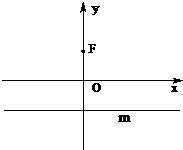 (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且