题目内容
10. 已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1.
已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1.(1)求证:AF⊥CE;
(2)求多面体EFG-ABCD的体积.
分析 (1)证明AF⊥平面CDGE,即可证明结论;
(2)多面体EFG-ABCD的体积=正方体ABCD-GPHF-四棱锥C-HFEP.
解答 (1)证明:连接DG,则AF⊥DG,
∵AF⊥CD,CD∩DG=D,
∴AF⊥平面CDGE,
∵CE?平面CDGE,
∴AF⊥CE;
(2)解:多面体EFG-ABCD的体积=正方体ABCD-GPHF-四棱锥C-HFEP
=23-$\frac{1}{3}×\frac{1}{2}×(1+2)×2$=7.
点评 本题主要考查空间线面的位置关系,多面体EFG-ABCD的体积的计算等基本知识,考查空间想象能力、逻辑思维能力、运算求解能力和探究能力.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$. 为偶函数,且当
为偶函数,且当 时,
时, ,则不等式
,则不等式 的解集为__________.
的解集为__________.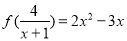 ,则
,则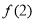 等于( )
等于( )