题目内容
13. 如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$.(Ⅰ)平面PAB⊥平面PBC;
(Ⅱ)E为BC上的一点.若直线AE与平面PBC所成的角为30°,求BE的长.
分析 (Ⅰ)证明BC⊥平面PAB,即可证明平面PAB⊥平面PBC;
(Ⅱ)取PB的中点F,连结EF,证明∠AEF是直线AE与平面PBC所成的角,利用直线AE与平面PBC所成的角为30°,即可求BE的长.
解答 
得AB=2
在△PBC中,PB=2,PC=4,∠BPC=60°,
由余弦定理,得BC=2$\sqrt{3}$
在△PAC中,PA=2,PC=4,cos∠APC=$\frac{1}{4}$,
由余弦定理,得AC=4
因为AB2+BC2=AC2,所以AB⊥BC …(4分)
又因为PB2+BC2=AC2,所以PB⊥BC
因为AB∩PB=B,所以BC⊥平面PAB …(6分)
又因为BC?平面PBC,所以平面PAB⊥平面PBC …(7分)
(Ⅱ)取PB的中点F,连结EF,则AF⊥PB.
又因为平面PAB⊥平面PBC,平面PAB∩平面PBC=PB,AF?平面PAB,
所以AF⊥平面PBC
因此∠AEF是直线AE与平面PBC所成的角,即∠AEF=30° …(11分)
在正△PAB中,AF=$\frac{\sqrt{3}}{2}$PA=$\sqrt{3}$.
在Rt△AEF中,AE=$\frac{AF}{sin30°}$=2$\sqrt{3}$
在Rt△ABE中,BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=2$\sqrt{2}$ …(15分)
点评 本题考查线面垂直、平面与平面垂直的判定,考查直线与平面所成的角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
6.若x,y满足$\left\{\begin{array}{l}x+y≥0\\ x≥1\\ x-y≥0\end{array}\right.$,则下列不等式恒成立的是( )
| A. | y≥-1 | B. | x≥2 | C. | x+2y+2≥0 | D. | 2x-y+1≥0 |
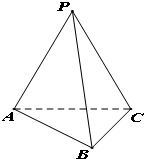 如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.
如图,在三棱锥P-ABC中,平面APC⊥平面ABC,且PA=PB=PC=4,AB=BC=2.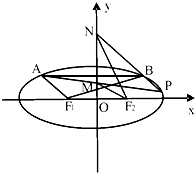 如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.
如图,F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且焦距为2$\sqrt{2}$,动弦AB平行于x轴,且|F1A|+|F2A|=4.
 B.
B.
 D.
D.
 已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1.
已知棱长为2的正方体ABCD-GPHF截去一个多面体后,所得几何体如图所示,点E在GP上,且EG=1.