题目内容
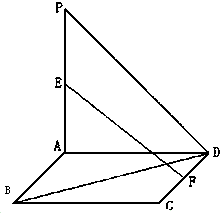 如图,PA⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.
如图,PA⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD,E、F分别是线段PA、CD的中点.(1)求EF和平面ABCD所成的角α;
(2)求异面直线EF与BD所成的角β.
分析:(1)由已知可得EA⊥平面ABCD,连结AF,则∠EFA=α,设出PA=AD=2,通过解三角形求出α的正切值,则角α可求;
(2)在平面ABCD中,过F作FG∥BD,得到∠EFG为异面直线EF与BD所成的角β,解直角三角形求出边长后再利用余弦定理求角β的余弦值,则角β可求.
(2)在平面ABCD中,过F作FG∥BD,得到∠EFG为异面直线EF与BD所成的角β,解直角三角形求出边长后再利用余弦定理求角β的余弦值,则角β可求.
解答: 解:(1)如图,
解:(1)如图,
∵PA⊥平面ABCD,E∈PA,∴EA⊥平面ABCD.
∴EF和平面ABCD所成的角α即为∠EFA.
设PA=AD=2,∵E、F分别是线段PA、CD的中点,
则EA=DF=1,在Rt△ADF中,AF=
=
=
.
在Rt△EAF中,tanα=tan∠EFA=
=
=
.
所以α=arctan
;
(2)在平面ABCD中,过F作FG∥BD,∴G为BC中点.
异面直线EF与BD所成的角β即为∠EFG.
连结EG,
在Rt△ABG中,AG=
=
=
.
在Rt△EAG中,EG=
=
=
.
同理求得EF=
.
在Rt△GCF中,GF=
=
.
则在△EFG中,cosβ=cos∠EFG=
=
=
.
所以β=arccos
.
 解:(1)如图,
解:(1)如图,∵PA⊥平面ABCD,E∈PA,∴EA⊥平面ABCD.
∴EF和平面ABCD所成的角α即为∠EFA.
设PA=AD=2,∵E、F分别是线段PA、CD的中点,
则EA=DF=1,在Rt△ADF中,AF=
| AD2+DF2 |
| 22+12 |
| 5 |
在Rt△EAF中,tanα=tan∠EFA=
| EA |
| AF |
| 1 | ||
|
| ||
| 5 |
所以α=arctan
| ||
| 5 |
(2)在平面ABCD中,过F作FG∥BD,∴G为BC中点.
异面直线EF与BD所成的角β即为∠EFG.
连结EG,
在Rt△ABG中,AG=
| AB2+BG2 |
| 22+12 |
| 5 |
在Rt△EAG中,EG=
| EA2+AG2 |
12+(
|
| 6 |
同理求得EF=
| 6 |
在Rt△GCF中,GF=
| 12+12 |
| 2 |
则在△EFG中,cosβ=cos∠EFG=
| EF2+FG2-EG2 |
| 2•EF•FG |
(
| ||||||
2×
|
| ||
| 6 |
所以β=arccos
| ||
| 6 |
点评:本题考查了直线和平面所成的角,考查了异面直线所成的角,考查了学生的空间想象和思维能力,解答的关键是角的找取,训练了利用反三角函数表示角,是中档题.

练习册系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.